Next: Reflection Up: Modelling of obstacles Previous: Modelling of obstacles
There are several mechanisms for transmission of waves. In SWAN, the user may compute transmission of waves passing
over a dam with a closed surface or may choose a constant transmission coefficient.
If the crest of the breakwater is at a level
where (at least part of the) waves can pass over, the transmission coefficient 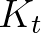 (defined as the ratio of
the (significant) wave height at the downwave side of the dam over the (significant) wave height at the
upwave side) is a function of wave height and the difference in crest level and water level. It must be noted that
the transmission coefficient can never be smaller than 0 or larger than 1. In SWAN, two expressions
can be employed. The first is taken from Goda et al. (1967):
(defined as the ratio of
the (significant) wave height at the downwave side of the dam over the (significant) wave height at the
upwave side) is a function of wave height and the difference in crest level and water level. It must be noted that
the transmission coefficient can never be smaller than 0 or larger than 1. In SWAN, two expressions
can be employed. The first is taken from Goda et al. (1967):
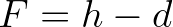 is the freeboard of the dam and where
is the freeboard of the dam and where 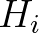 is the incident (significant) wave height at the
upwave side of the obstacle (dam),
is the incident (significant) wave height at the
upwave side of the obstacle (dam), 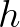 is the crest level of the dam above the reference level (same as
reference level of the bottom),
is the crest level of the dam above the reference level (same as
reference level of the bottom), 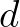 the mean water level relative to the reference level, and the coefficients
the mean water level relative to the reference level, and the coefficients
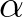 ,
, 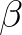 depend on the shape of the dam (Seelig, 1979) as given in Table 2.1. It should be
noted that this formula is only valid for slopes more gentle than 1:0.7 (1.4:1 or 55 degrees).
depend on the shape of the dam (Seelig, 1979) as given in Table 2.1. It should be
noted that this formula is only valid for slopes more gentle than 1:0.7 (1.4:1 or 55 degrees).
| case | 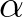 |
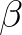 |
||
| vertical thin wall | 1.8 | 0.1 | ||
| caisson | 2.2 | 0.4 | ||
| dam with slope 1:3/2 | 2.6 | 0.15 |
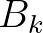 the crest width and
the crest width and
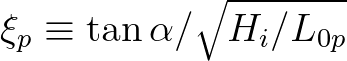 the breaker parameter. For this,
the slope of the breakwater
the breaker parameter. For this,
the slope of the breakwater 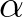 must be given and
must be given and
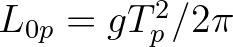 is the deep water wave length.
The restriction to eq. (2.173) is as follows
is the deep water wave length.
The restriction to eq. (2.173) is as follows
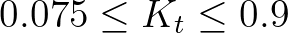 (2.173)
(2.173)
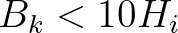 . However, if this is not the case, the following expression
should be used instead of (2.173):
. However, if this is not the case, the following expression
should be used instead of (2.173):
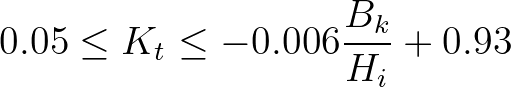 (2.175)
(2.175)
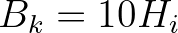 . Following
Van der Meer et al. (2005), for practical
application, Eq. (2.173) is applied if
. Following
Van der Meer et al. (2005), for practical
application, Eq. (2.173) is applied if 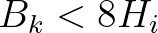 , Eq. (2.175) if
, Eq. (2.175) if 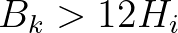 and
in between (
and
in between (
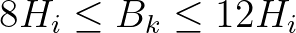 ), a linear interpolation is carried out.
), a linear interpolation is carried out.
The SWAN team 2024-09-09