Next: Numerical approach Up: Implementation of 2D wave Previous: Implementation of 2D wave
Wave setup is usually confined to narrow zones in the immediate vicinity of the
shoreline. The size of such areas is small enough that the setup process can be
considered to be quasi-stationary.
Wave-induced currents are usually weak compared to tidal currents.
This implies
an equilibrium between the wave-induced force and gradient of the wave setup,
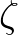 is the setup,
is the setup, 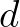 the water depth and
the water depth and 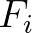 is the wave-induced force in
is the wave-induced force in 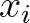 -direction per unit mass.
In order to reduce the number of equations to one, we use the observation by
Dingemans (1997) that wave-driven currents are mainly due to the
divergence-free part of the wave forces whereas the setup is mainly due to the
rotation-free part of the force field. We therefore take the divergence of eq. (5.1) to
obtain the following elliptic partial differential equation for
-direction per unit mass.
In order to reduce the number of equations to one, we use the observation by
Dingemans (1997) that wave-driven currents are mainly due to the
divergence-free part of the wave forces whereas the setup is mainly due to the
rotation-free part of the force field. We therefore take the divergence of eq. (5.1) to
obtain the following elliptic partial differential equation for 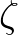 ,
,
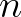 the outward direct normal.
It is not possible to use this boundary condition on all boundary points because
then there remains an unknown constant. So some point for which we take the
boundary point with the largest depth, the setup is assumed to be
the outward direct normal.
It is not possible to use this boundary condition on all boundary points because
then there remains an unknown constant. So some point for which we take the
boundary point with the largest depth, the setup is assumed to be 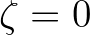 .
.
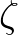 is also used in nested
models. The setup computed in the larger model is used as boundary condition in
the nested model. In the nested model the setup is given in all points of the outer
boundary. On the shoreline inside the area again eq. (5.3) is used.
is also used in nested
models. The setup computed in the larger model is used as boundary condition in
the nested model. In the nested model the setup is given in all points of the outer
boundary. On the shoreline inside the area again eq. (5.3) is used.
The SWAN team 2024-09-09