Next: Successive Over Relaxation (SOR) Up: Iterative solvers Previous: Iterative solvers
We want to solve the following linear system of equations
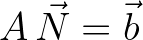 (6.1)
(6.1)
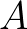 is some non-symmetric penta-diagonal matrix,
is some non-symmetric penta-diagonal matrix, 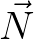 is the wave action vector to be solved and
is the wave action vector to be solved and 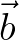 contains source terms and boundary values.
contains source terms and boundary values.
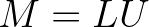 is a good approximation to the
matrix
is a good approximation to the
matrix 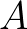 , rapid convergence results. These observations lead to the idea
of using an approximate LU factorization of
, rapid convergence results. These observations lead to the idea
of using an approximate LU factorization of 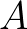 as the iteration matrix
as the iteration matrix 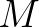 , i.e.:
, i.e.:
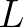 and
and 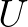 are both sparse and
are both sparse and 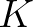 is small. For non-symmetric matrices the incomplete LU
(ILU) factorisation gives such an decomposition but unfortunately converges rather slowly. In
the ILU method one proceeds as in a standard LU decomposition. However, for every element
of the original matrix
is small. For non-symmetric matrices the incomplete LU
(ILU) factorisation gives such an decomposition but unfortunately converges rather slowly. In
the ILU method one proceeds as in a standard LU decomposition. However, for every element
of the original matrix 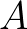 that is zero the corresponding elements in
that is zero the corresponding elements in 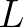 or
or 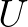 is set to zero. This
means that the product of
is set to zero. This
means that the product of 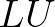 will contain more nonzero diagonals than the original matrix
will contain more nonzero diagonals than the original matrix 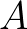 .
Therefore the matrix
.
Therefore the matrix 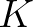 must contain these extra diagonals as well if Eq. (6.2) is to hold.
must contain these extra diagonals as well if Eq. (6.2) is to hold.
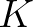 to have more non zero entries on all seven diagonals and using the interpolation
mentioned above the SIP method constructs an LU factorization with the property that for a
given approximate solution
to have more non zero entries on all seven diagonals and using the interpolation
mentioned above the SIP method constructs an LU factorization with the property that for a
given approximate solution 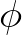 the product
the product
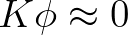 and thus the iteration matrix
and thus the iteration matrix 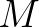 is close to
is close to
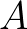 by relation (6.2).
by relation (6.2).
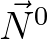 an iteration is performed solving:
an iteration is performed solving:
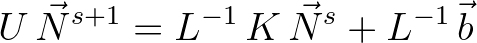 (6.3)
(6.3)
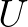 is upper triangular this equation is efficiently solved by back substitution.
An essential property which makes the method feasible is that the matrix
is upper triangular this equation is efficiently solved by back substitution.
An essential property which makes the method feasible is that the matrix 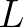 is easily
invertible. This iterative process is repeated
is easily
invertible. This iterative process is repeated
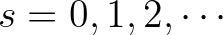 until convergence is reached.
until convergence is reached.
The SWAN team 2024-09-09