Next: Conditions imposed to the Up: Description of an unstructured Previous: Definitions
For a two-dimensional triangular mesh, the number of cells 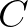 , the number of boundary faces
, the number of boundary faces 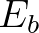 and internal faces
and internal faces 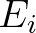 are related according to:
are related according to:
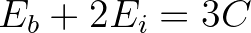 (8.1)
(8.1)
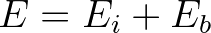 . With
. With 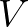 the number of vertices and
the number of vertices and 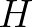 the number of holes ('islands'), we have the following Euler's relation
for a triangulation:
the number of holes ('islands'), we have the following Euler's relation
for a triangulation:
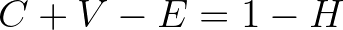 (8.2)
(8.2)
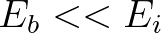 and the number of holes
and the number of holes 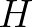 is negligibly small, so
is negligibly small, so
 (8.3)
(8.3)