Next: Numerical method Up: Unstructured mesh implementation Previous: Conditions imposed to the
We briefly outline some issues related to grid generation from a practical point of view.
The process of grid generation can be difficult and time consuming. A common approach is proceeding from coarse to fine grid through refinement in various ways.
Generally, one would like to have an optimal grid in which areas where the bathymetry or evolution of the waves change
rapidly require a higher resolution than areas where the physics or depth changes less.
This goes around by having an indication how to determine the refinement based on
bathymetry or geometric variations through preliminary evaluations.
To facilitate this procedure,
many user-friendly mesh generation packages are available on the Internet. In addition, there are public-domain, graphical Matlab and Python interfaces
to Triangle (Shewchuk, 1996).
Triangle is a freely-distributed, two-dimensional Delaunay triangulator and is widely utilized.
An important key ingredient for the preparation of the grid for the wave model domain is bathymetry data.
Boundary nodes, segments and holes
can be created from this data with the
use of the mesh editing options of a mesh generation package.
After checking and improving grid quality, the final information on nodes and segments is forced into the
triangulation of the domain.
This triangulation includes only acute triangles.
A good grid generator provides many pre-defined depth-dependent contraints for further mesh refinement.
From a numerical point of view, mesh refinement is often directly related to properly resolve the shape of the wave,
i.e. to keep the wavelength to grid size ratio relatively large.
When wavelength decreases in shallower water, the grid size must decrease as well. Therefore, this criterion, called the 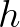 -refinement,
has the effect of using smaller cells in shallow water and larger
cells in deeper water. Here,
-refinement,
has the effect of using smaller cells in shallow water and larger
cells in deeper water. Here, 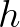 refers to the water depth. Another useful criterion is known as the topographic length scale constraint,
when one try to keep the ratio
refers to the water depth. Another useful criterion is known as the topographic length scale constraint,
when one try to keep the ratio 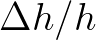 less than one. Here,
less than one. Here, 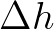 equals the difference between the maximum depth of a triangle and the minimum depth and
equals the difference between the maximum depth of a triangle and the minimum depth and
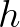 is the average depth. This
criterion addresses the bathymetric slope and cells with a high value of
is the average depth. This
criterion addresses the bathymetric slope and cells with a high value of 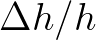 indicate areas of steep bottom topography that will need to be
more finely resolved.
When refining the grid, one must balance the need to fully meet the refinement criteria with the desire to keep the triangle sizes from becoming too small.
Thus, these criteria
are generally imposed along with a minimum area constraint.
The refinement process is repeated iteratively until a final grid with the appropriate resolution is obtained.
indicate areas of steep bottom topography that will need to be
more finely resolved.
When refining the grid, one must balance the need to fully meet the refinement criteria with the desire to keep the triangle sizes from becoming too small.
Thus, these criteria
are generally imposed along with a minimum area constraint.
The refinement process is repeated iteratively until a final grid with the appropriate resolution is obtained.
The SWAN team 2024-09-09