Next: Output grids Up: Choice of grids, time Previous: Input grid(s) and time Index
The computational spatial grid must be defined by the user. The orientation (direction) can be chosen
arbitrarily.
The boundaries of the computational spatial grid in SWAN are either land or water. In the case of land
there is no problem: the land does not generate waves and in SWAN it absorbs all incoming wave energy.
But in the case of a water boundary there may be a problem. Often no wave conditions are known along
such a boundary and SWAN then assumes that no waves enter the area and that waves can leave the
area freely. These assumptions obviously contain errors which propagate into the model. These
boundaries must therefore be chosen sufficiently far away from the area where reliable computations are
needed so that they do not affect the computational results there. This is best established by varying the
location of these boundaries and inspect the effect on the results. Sometimes the waves at these boundaries
can be estimated with a certain degree of reliability. This is the case if (a) results of another
model run are available (nested computations) or, (b) observations are available. If model results are
available along the boundaries of the computational spatial grid, they are usually from a coarser
resolution than the computational spatial grid under consideration. This implies that this coarseness of
the boundary propagates into the computational grid. The problem is therefore essentially the same as
if no waves are assumed along the boundary except that now the error may be more acceptable (or the
boundaries are permitted to be closer to the area of interest). If observations are available, they can be
used as input at the boundaries. However, this usually covers only part of the boundaries so that the rest
of the boundaries suffer from the same error as above.
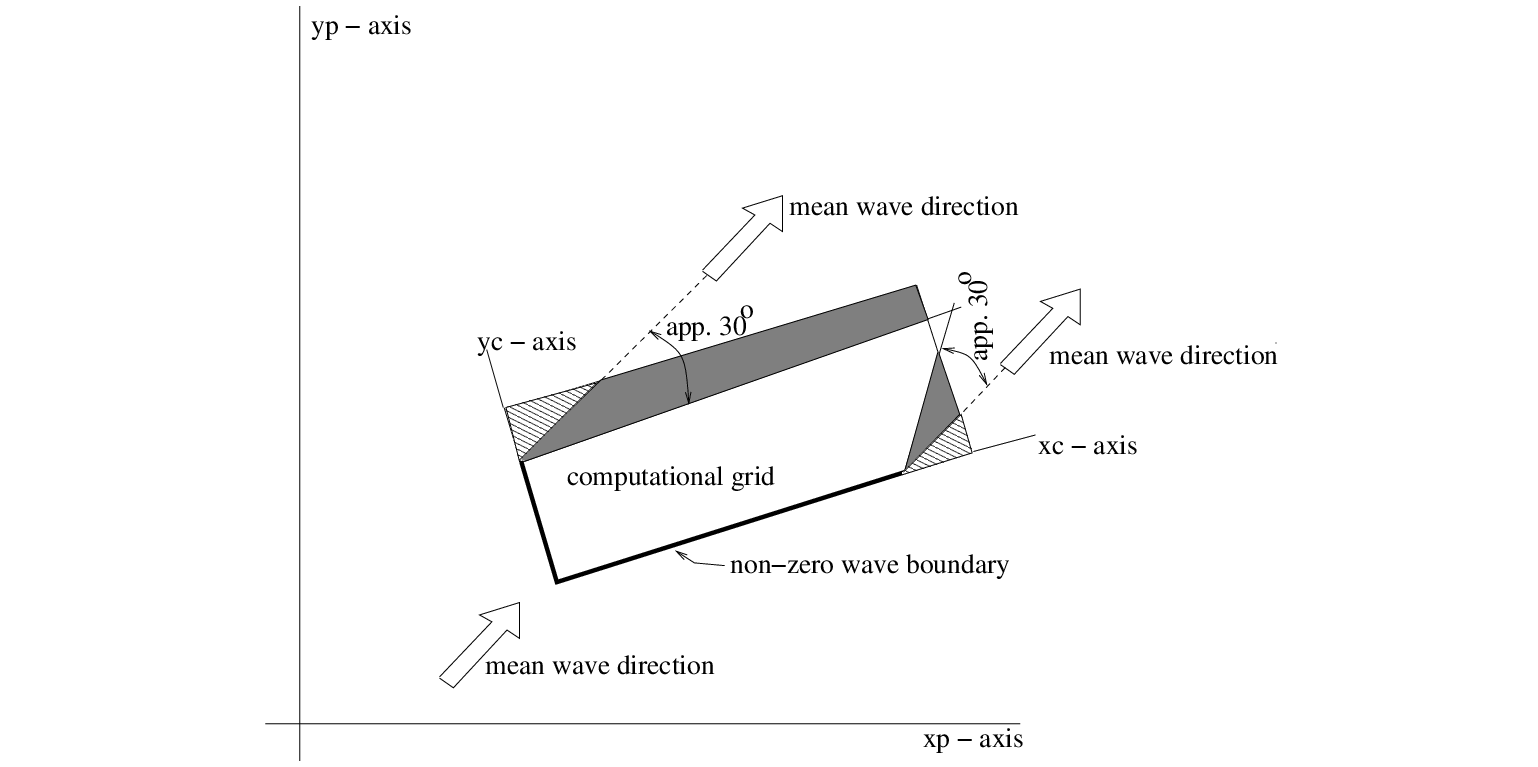
A special case occurs near the coast. Here it is often possible to identify an up-wave boundary (with
proper wave information) and two lateral boundaries (with no or partial wave information). The affected
areas with errors are typically regions with the apex at the corners of the water boundary with wave
information, spreading towards shore at an angle of 30 to 45
to 45 for wind sea conditions
to either side of the imposed mean wave direction (less for swell conditions; the angle is essentially the
one-sided width of the directional distribution of wave energy). For propagation of short crested waves
(wind sea condtions) an example is given in Figure 2.1. For this reason the lateral boundaries
should be sufficiently far away from the area of interest to avoid the propagation of this error into this area.
Such problems do not occur if the lateral boundaries contain proper wave information over their entire length
e.g. obtained from a previous SWAN computation or if the lateral boundaries are coast.
for wind sea conditions
to either side of the imposed mean wave direction (less for swell conditions; the angle is essentially the
one-sided width of the directional distribution of wave energy). For propagation of short crested waves
(wind sea condtions) an example is given in Figure 2.1. For this reason the lateral boundaries
should be sufficiently far away from the area of interest to avoid the propagation of this error into this area.
Such problems do not occur if the lateral boundaries contain proper wave information over their entire length
e.g. obtained from a previous SWAN computation or if the lateral boundaries are coast.
 |
When output is requested along a boundary of the computational grid, it may occur
that this output differs from the boundary conditions that are imposed by the user. The reason is that
SWAN accepts only the user-imposed incoming wave components and that it replaces the user-imposed
outgoing wave components with computed outgoing components (propagating to the boundary from
the interior region). The user is informed by means of a warning in the output when the
computed significant wave height differs more than 10%, say (10% is default), from the user-imposed
significant wave height (command BOUND...). The actual value of this difference can be set by the
user (see the SET command). Note that this warning will not apply in the case of unstructured grids.
If the computational grid extends outside the input grid, the reader is referred to Section 2.6.2
to find the assumptions of SWAN on depth, current, water level, wind, bottom friction, vegetation, mud, and ice
in the non-overlapping area.
The spatial resolution of the computational grid should be sufficient to resolve relevant details of the wave
field. Usually a good choice is to take the resolution of the computational grid approximately equal to that
of the bottom or current grid. If necessary, an unstructured grid may be used.
SWAN may not use the entire user-provided computational grid if the user defines exception values on
the depth grid (see command INPGRID BOTTOM) or on the curvilinear computational grid (see command
CGRID).
A computational grid point is either
 generation mode of SWAN. The initial condition of a nonstationary run of SWAN
is by default a JONSWAP spectrum with a
generation mode of SWAN. The initial condition of a nonstationary run of SWAN
is by default a JONSWAP spectrum with a
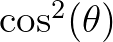 directional distribution centred around the
local wind direction.
directional distribution centred around the
local wind direction.
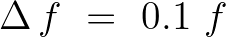 ). The frequency domain may
be specified as follows (see command CGRID):
). The frequency domain may
be specified as follows (see command CGRID):
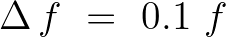 . This resolution is required
by the DIA method for the approximation of nonlinear 4-wave interactions (the so-called quadruplets).
. This resolution is required
by the DIA method for the approximation of nonlinear 4-wave interactions (the so-called quadruplets).
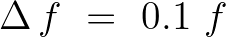 . This resolution is required by
the DIA method for the approximation of nonlinear 4-wave interactions.
. This resolution is required by
the DIA method for the approximation of nonlinear 4-wave interactions.
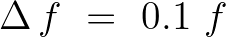 . This resolution is required
by the DIA method for the approximation of nonlinear 4-wave interactions.
. This resolution is required
by the DIA method for the approximation of nonlinear 4-wave interactions.
 unless the user specifies a
limited directional range. This may be convenient (less computer time and/or memory space), for example,
when waves travel towards a coast within a limited sector of 180
unless the user specifies a
limited directional range. This may be convenient (less computer time and/or memory space), for example,
when waves travel towards a coast within a limited sector of 180 . The directional resolution
is determined by the number of discrete directions that is provided by the user. For wind seas with a
directional spreading of typically 30
. The directional resolution
is determined by the number of discrete directions that is provided by the user. For wind seas with a
directional spreading of typically 30 on either side of the mean wave direction, a resolution
of 10
on either side of the mean wave direction, a resolution
of 10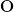 seems enough whereas for swell with a directional spreading of less than 10
seems enough whereas for swell with a directional spreading of less than 10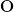 ,
a resolution of 2
,
a resolution of 2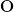 or less may be required. If the user is confident that no energy will occur
outside a certain directional sector (or is willing to ignore this amount of energy), then the computations
by SWAN can be limited to the directional sector that does contain energy. This may often be the case of
waves propagating to shore within a sector of 180
or less may be required. If the user is confident that no energy will occur
outside a certain directional sector (or is willing to ignore this amount of energy), then the computations
by SWAN can be limited to the directional sector that does contain energy. This may often be the case of
waves propagating to shore within a sector of 180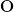 around some mean wave direction.
around some mean wave direction.
| direction resolution for wind sea |
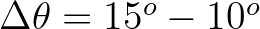 |
|
| direction resolution for swell |
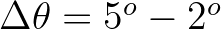 |
|
| frequency range |
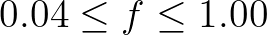 Hz Hz |
|
| spatial resolution |
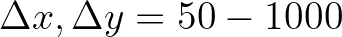 m m |
The numerical schemes in the SWAN model require a minimum number of discrete grid points in each
spatial directions of 2. The minimum number of directional bins is 3 per directional quadrant and
the minimum number of frequencies should be 4.
A final remark on the choice of spatial and spectral resolution. SWAN should not shift energy more than
one spectral bin (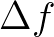 and/or
and/or 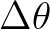 ) when propagating over one spatial grid cell
(
) when propagating over one spatial grid cell
(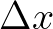 and/or
and/or 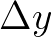 ). This is for reasons for accuracy and not stability. See for details
Section 3.8 of the Scientific/Technical documentation. This implies that although SWAN will be stable,
whatever resolution you choose, you need to balance spectral and spatial resolution. This could mean,
i.e. not necessarily, that you have to refine your spatial resolution when you refine your spectral
resolution.
). This is for reasons for accuracy and not stability. See for details
Section 3.8 of the Scientific/Technical documentation. This implies that although SWAN will be stable,
whatever resolution you choose, you need to balance spectral and spatial resolution. This could mean,
i.e. not necessarily, that you have to refine your spatial resolution when you refine your spectral
resolution.
In a situation with currents this is particularly important at the highest frequencies
where the Doppler shifts are largest.
However, it may well be that inaccuracies thus generated will be removed by the source terms.
In other words, accurate Doppler shifts at high frequencies require high spectral and spatial
resolution, but the effects may be dominated by white capping. Hence, at the high frequencies,
the problem is perhaps masked by white capping. The inaccuracies may only appear at the lowest
frequencies, where usually the source terms are relatively weak at these frequencies.
Another issue concerns the excessive wave turning of relatively long waves at shallow water, or
cases with depth varies considerably over one spatial grid step, e.g. at the edge of shelf break
or seamount at deep ocean. As the refraction becomes excessive in a region with steep bottom gradients,
it is possible that the wave energy focus toward a single grid point, creating unrealistically large
wave heights and long periods; see Dietrich et al. (2013).
SWAN can optionally uses a Courant-type limiter (see command NUMERIC). This limiter is locally
in geographic space for cosmetic reasons, but it avoids propagating a large error to the rest of the
geographic domain and thus improve the solution there. However, if the limiter is activated, the
computation is still inaccurate, but less so as you are farther from the location with poor resolution.
The common mistake people often make is that the limiter may affect the model results negatively,
which is, however, not entirely true. As the resolution is too coarse, the model results are inaccurate
anyway. Hence, the proper solution to this problem is to choose a suitable resolution, both spectral
and spatial, and one can thus avoid the use of the limiter.
The SWAN team 2024-09-09