Several types of grids and time window(s) need to be defined: (a) spectral grid, (b) spatial (geographic)
grids and time window(s) in case of nonstationary computations.
The spectral grid that need to be defined by the user is a computational spectral grid on
which SWAN performs the computations.
SWAN has the option to make computations that can be nested in (coarse) SWAN, WAM or WAVEWATCH
III. In such cases, the spectral grid need not be equal to the spectral grid in the coarse SWAN, WAM or
WAVEWATCH III run.
The spatial grids that need to be defined by the user are (if required):
- a computational spatial grid on which SWAN performs the computations,
- one (or more) spatial input grid(s) for the bottom, current field, water level,
bottom friction, vegetation, mud, sea ice and wind (each input grid may differ from the others) and
- one (or more) spatial output grid(s) on which the user requires output of SWAN.
The wind, bottom friction, vegetation, mud and sea ice do not require a grid if they are uniform over
the area of interest.
For one-dimensional situations, i.e.
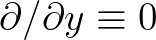 , SWAN can be run in 1D mode.
, SWAN can be run in 1D mode.
If a uniform, rectangular computational spatial grid is chosen in SWAN, then all input and output
grids must be uniform and rectangular too, but they may all be different from each other.
If a curvilinear computational spatial grid is chosen in SWAN, then each input grid
should be either uniform, rectangular or identical to the used curvilinear grid or staggered with
respect to the curvilinear computational grid.
If an unstructured computational spatial grid is chosen in SWAN, then each input grid
should be either uniform, rectangular or identical to the used unstructured grid.
SWAN has the option to make computations that are nested in (coarse) SWAN, WAM or WAVEWATCH III.
In such runs, SWAN interpolates the spatial boundary of the SWAN, WAM or WAVEWATCH III grid to the
(user provided) grid of SWAN (that needs to (nearly) coincide along the grid lines of WAM or WAVEWATCH
III or the output nest grid boundaries of SWAN). Since, the computational grids of WAM and WAVEWATCH
III are in spherical coordinates, it is recommended to use spherical coordinates in a nested SWAN when
nesting in WAM or WAVEWATCH III.
SWAN using an unstructured mesh may be nested in SWAN employing a regular grid and
vice versa. However, SWAN using an unstructured grid cannot be nested in WAM or WAVEWATCH III.
Nesting from a 2D model to a 1D model is possible although is should not be done by using the
commands NGRID and NEST. Instead, define the boundary point of the 1D model as an output
point (using command POINTS) and write the spectra for that point using the command SPECout.
In the 1D model, this spectra is used as boundary condition using the BOUNDSPEC command.
Similarly, the wind fields may be available in different time windows than the current and water
level fields and the computations may need to be carried out at other times than these input fields.
For these reasons SWAN operates with different time windows with different time steps (each may have
a different start and end time and time step):
- one computational time window in which SWAN performs the computations,
- one (or more) input time window(s) in which the bottom, current field, water level,
bottom friction, vegetation, mud, sea ice and wind field (if present) are given by the user
(each input window may differ form the others) and
- one (or more) output time window(s) in which the user requires output of SWAN.
In case of nesting, SWAN searches the boundary conditions in the relevant output file of the previous
SWAN, WAM or WAVEWATCH III runs to take the boundary conditions at the start time of the nested run.
It will not take the initial condition (i.e. over the entire computational grid) for the nested run
from the previous SWAN, WAM or WAVEWATCH III run.
During the computation SWAN obtains bottom, current, water level, wind, bottom friction, vegetation, mud and sea ice
information by tri-linear interpolation from the given input grid(s) and time window(s). The output is
in turn obtained in SWAN by bi-linear interpolation in space from the computational grid; there is no interpolation
in time, the output time is shifted to the nearest computational time level. Interpolation errors can be
reduced by taking the grids and windows as much as equal to one another as possible (preferably identical).
It is recommended to choose output times such that they coincide with computational time levels.
The SWAN team 2024-09-09
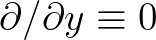 , SWAN can be run in 1D mode.
, SWAN can be run in 1D mode.