General concepts
In shallow water, six basic processes contribute to 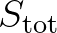 :
:
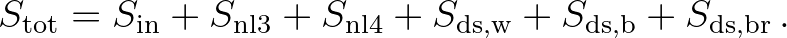 (2.28)
(2.28)
These terms denote, respectively, wave growth by the wind, nonlinear transfer of wave energy
through three-wave and four-wave interactions and wave decay due to whitecapping, bottom friction
and depth-induced wave breaking. First, a brief summary of the formulations is given below. Next,
for each term complete expressions are outlined.
Wind input
Transfer of wind energy to the waves is described with a resonance mechanism (Phillips, 1957) and a
feed-back mechanism (Miles, 1957).
Resonance with wind-induced pressure fluctations
The pressure distribution induced by wind at the sea surface is random. It propagates
more or less a frozen pattern over the surface with wind speed. This can be Fourier
transformed to produce harmonic pressure waves that propagate with wind speed. If this
harmonic pressure wave remains in phase with a free harmonic surface wave, then
the wind energy is transferred from the pressure wave to the surface wave. The energy
input by this mechanism, which contributes to the initial stages of wave growth,
varies linearly with time.
Feedback of wave-induced pressure fluctations
When a wave has been generated by the resonance mechanism as explained above, it will
distort the wind profile just above the water surface. This distortion results in an
'over pressure' on the wind ward side of the crest of the wave and an 'under pressure'
at the lee side of the crest. It means that when the sea surface moves up and down,
the pressure also follows the same movements, therefore transfer energy to the wave.
This energy transfer is proportional to the energy in the wave itself, so the wave
grows more as it gets larger. This effect is found to be exponential in time.
Based on the two wave growth mechanisms, wave growth due to wind commonly described
as the sum of linear and exponential growth term of a wave component:
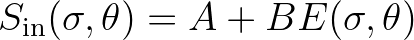 (2.29)
(2.29)
in which 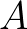 and
and 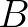 depend on wave frequency and direction, and wind speed and direction. The effects of
currents are accounted for by using the apparent local wind speed and direction. The expression
for the term
depend on wave frequency and direction, and wind speed and direction. The effects of
currents are accounted for by using the apparent local wind speed and direction. The expression
for the term 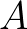 is due to Cavaleri and Malanotte-Rizzoli (1981) with a filter to avoid growth at frequencies
lower than the Pierson-Moskowitz frequency (Tolman, 1992a). Two optional expressions for the coefficient
is due to Cavaleri and Malanotte-Rizzoli (1981) with a filter to avoid growth at frequencies
lower than the Pierson-Moskowitz frequency (Tolman, 1992a). Two optional expressions for the coefficient
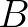 are used in the SWAN model. The first is taken from an early version of the WAM Cycle 3 model
(the WAMDI group, 1988). It is due to Snyder et al. (1981), rescaled in terms of friction velocity
are used in the SWAN model. The first is taken from an early version of the WAM Cycle 3 model
(the WAMDI group, 1988). It is due to Snyder et al. (1981), rescaled in terms of friction velocity
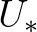 by Komen et al. (1984). The drag coefficient to relate
by Komen et al. (1984). The drag coefficient to relate 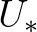 to the driving wind speed at 10 m elevation
to the driving wind speed at 10 m elevation
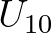 is taken from either Wu (1982) or Zijlema et al. (2012). The second expression for
is taken from either Wu (1982) or Zijlema et al. (2012). The second expression for 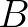 in SWAN is taken from the
WAM Cycle 4 model (Komen et al., 1994). It is due to Janssen (1991a) and it accounts
explicitly for the interaction between the wind and the waves by considering atmospheric boundary layer
effects and the roughness length of the sea surface. The corresponding set of equations is solved (as
in the WAM model) with the iterative procedure of Mastenbroek et al. (1993).
in SWAN is taken from the
WAM Cycle 4 model (Komen et al., 1994). It is due to Janssen (1991a) and it accounts
explicitly for the interaction between the wind and the waves by considering atmospheric boundary layer
effects and the roughness length of the sea surface. The corresponding set of equations is solved (as
in the WAM model) with the iterative procedure of Mastenbroek et al. (1993).
Dissipation
The dissipation term of wave energy is represented by the summation of three different contributions:
whitecapping 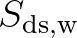 , bottom friction
, bottom friction 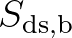 and depth-induced breaking
and depth-induced breaking 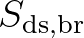 .
.
Whitecapping is primarily controlled by the steepness of the waves. In presently operating third-generation
wave models, the whitecapping formulations are based on a pulse-based model (Hasselmann, 1974), as adapted by the
WAMDI group (1988):
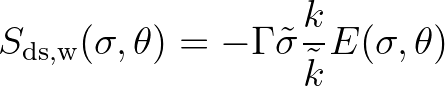 (2.30)
(2.30)
where 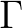 is a steepness dependent coefficient,
is a steepness dependent coefficient, 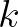 is wave number and
is wave number and
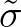 and
and 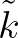 denote a mean frequency and a mean wave number, respectively (cf. the WAMDI group, 1988). Komen et al. (1984)
estimated the value of
denote a mean frequency and a mean wave number, respectively (cf. the WAMDI group, 1988). Komen et al. (1984)
estimated the value of 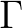 by closing the energy balance of the waves in fully developed conditions. This
implies that this value depends on the wind input formulation that is used. Since two expressions are used for the wind
input in SWAN, also two values for
by closing the energy balance of the waves in fully developed conditions. This
implies that this value depends on the wind input formulation that is used. Since two expressions are used for the wind
input in SWAN, also two values for 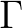 are used. The first is due to Komen et al. (1984), as in WAM Cycle 3.
The second expression is an adaptation of this expression based on Janssen (1991a), as in WAM Cycle 4
(see Janssen, 1991b; Günther et al., 1992). Young and Banner (1992) and Banner and Young (1994) have shown that
the results of closing the energy balance in this manner depend critically on the choice of a high-frequency cut-off
frequency above which a diagnostic spectral tail is used. In SWAN, this cut-off frequency is different from
the one used in the WAM model. Differences in the growth rates between the WAM model and SWAN are therefore to be
expected.
are used. The first is due to Komen et al. (1984), as in WAM Cycle 3.
The second expression is an adaptation of this expression based on Janssen (1991a), as in WAM Cycle 4
(see Janssen, 1991b; Günther et al., 1992). Young and Banner (1992) and Banner and Young (1994) have shown that
the results of closing the energy balance in this manner depend critically on the choice of a high-frequency cut-off
frequency above which a diagnostic spectral tail is used. In SWAN, this cut-off frequency is different from
the one used in the WAM model. Differences in the growth rates between the WAM model and SWAN are therefore to be
expected.
A number of alternative whitecapping expressions have been proposed to improve the accuracy of SWAN. These range
from alternative calibrations of the Komen et al. (1984) expression, e.g. Rogers et al. (2003), to
alternative ways of calculating mean spectral steepness, e.g. Van Vledder and Hurdle (2002).
In SWAN, another alternative is presented.
This alternative is proposed by Van der Westhuysen et al. (2007) and Van der Westhuysen (2007),
based on the whitecapping expression of Alves and Banner (2003). This expression is based
on experimental findings that whitecapping dissipation appears to be related to the nonlinear hydrodynamics within
wave groups. This yields a dissipation term that primarily depends on quantities that are local in the frequency
spectrum, as opposed to ones that are distributed over the spectrum, as in the expression of Komen et al. (1984).
However, the final whitecapping expression proposed by Alves and Banner (2003) features additional dependencies on
the spectral mean wavenumber and steepness, which is problematic in situations of mixed sea and swell often
encountered in the nearshore. Therefore, their whitecapping expression is applied in Van der Westhuysen (2007)
without these mean spectral dependencies. This adapted whitecapping expression is used together with a wind input
term that is based on that of Yan (1987).
In shallow water the orbital motions of the water particles, induced by surface waves, extend
down to the sea floor. This gives rise to an interaction between te surface waves and the
bottom. An overview of different wave-bottom interaction mechanisms and of their relative
strengths is given by Shemdin et al. (1978). They are: scattering on bottom irregularities,
motion of a soft bottom, percolation into a porous bottom and friction in the turbulent bottom
boundary layer. The first process results in a local redistribution of wave energy by
scattering of wave components. The last three are dissipative. Their strength depends on the
bottom conditions. For continental shelf seas with sandy bottoms, the dominant mechanism appears
to be bottom friction (Bertotti and Cavaleri, 1994) which can generally be expressed as
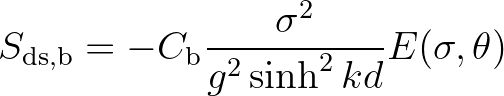 (2.31)
(2.31)
in which 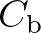 is a bottom friction coefficient. A large number of models has been proposed since the
pioneering paper of Putnam and Johnson (1949). Hasselmann et al. (1973) suggested to use an empirically
obtained constant. It seems to perform well in many different conditions as long as a suitable value is chosen
(typically different for swell and wind sea). A nonlinear formulation based on drag has been proposed by Hasselmann
and Collins (1968) which was later simplified by Collins (1972). More complicated, eddy viscosity models have been
developed by Madsen et al. (1988) and by Weber (1989, 1991a, 1991b). Considering the large variations in
bottom conditions in coastal areas (bottom material, bottom roughness length, ripple height, etc.), there
is no field data evidence to give preference to a particular friction model (Luo and Monbaliu, 1994). For
this reason, the simplest of each of these types of friction models has been implemented in SWAN: the
empirical JONSWAP model of Hasselmann et al. (1973), the drag law model of Collins (1972) and the
eddy-viscosity model of Madsen et al. (1988). The effect of a mean current on the wave energy dissipation
due to bottom friction is not taken into account in SWAN. The reasons for this are given by Tolman (1992b)
who argues that state-of-the-art expressions vary too widely in their effects to be acceptable. He found that
the error in finding a correct estimate of the bottom roughness length scale has a much larger impact on
the energy dissipation rate than the effect of a mean current.
is a bottom friction coefficient. A large number of models has been proposed since the
pioneering paper of Putnam and Johnson (1949). Hasselmann et al. (1973) suggested to use an empirically
obtained constant. It seems to perform well in many different conditions as long as a suitable value is chosen
(typically different for swell and wind sea). A nonlinear formulation based on drag has been proposed by Hasselmann
and Collins (1968) which was later simplified by Collins (1972). More complicated, eddy viscosity models have been
developed by Madsen et al. (1988) and by Weber (1989, 1991a, 1991b). Considering the large variations in
bottom conditions in coastal areas (bottom material, bottom roughness length, ripple height, etc.), there
is no field data evidence to give preference to a particular friction model (Luo and Monbaliu, 1994). For
this reason, the simplest of each of these types of friction models has been implemented in SWAN: the
empirical JONSWAP model of Hasselmann et al. (1973), the drag law model of Collins (1972) and the
eddy-viscosity model of Madsen et al. (1988). The effect of a mean current on the wave energy dissipation
due to bottom friction is not taken into account in SWAN. The reasons for this are given by Tolman (1992b)
who argues that state-of-the-art expressions vary too widely in their effects to be acceptable. He found that
the error in finding a correct estimate of the bottom roughness length scale has a much larger impact on
the energy dissipation rate than the effect of a mean current.
When waves propagate towards shore, shoaling leads to an increase in wave height. When the ratio
of wave height over water depth exceeds a certain limit, waves start to break, thereby dissipating
energy rapidly. In extreme shallow water (surf zone), this process becomes dominant over all other
processes. The process of depth-induced wave breaking is still poorly understood and little is
known about its spectral modelling. In contrast to this, the total dissipation (i.e. integrated
over the spectral space) due to this type of wave breaking can be well modelled with the dissipation
of a bore applied to the breaking waves
in a random field (Battjes and Janssen, 1978; Thornton and Guza, 1983). Laboratory observations (e.g.,
Battjes and Beji, 1992; Vincent et al. 1994; Arcilla et al., 1994 and Eldeberky and Battjes, 1996) show that
the shape of initially uni-modal spectra propagating across simple (barred) beach profiles, is fairly
insensitive to depth-induced breaking. This has led Eldeberky and Battjes (1995) to formulate a spectral
version of the bore model of Battjes and Janssen (1978) that conserves the spectral shape. Expanding
their expression to include directions, the expression reads:
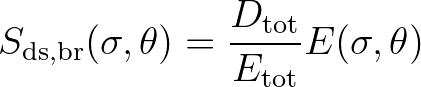 (2.32)
(2.32)
in which 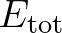 is the total wave energy and
is the total wave energy and
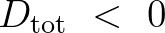 is the rate of dissipation of
the total energy due to wave breaking according to Battjes and Janssen (1978).
The value of
is the rate of dissipation of
the total energy due to wave breaking according to Battjes and Janssen (1978).
The value of 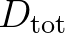 depends critically on the breaker parameter
depends critically on the breaker parameter
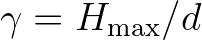 (in which
(in which 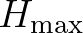 is the maximum possible individual wave height in the local water depth
is the maximum possible individual wave height in the local water depth 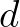 ).
In SWAN, both a constant value and a variable value are available. Examples of a variable breaker parameter
can be found in Nelson (1987) and Ruessink et al. (2003). (Both are implemented in SWAN.)
The constant value is
).
In SWAN, both a constant value and a variable value are available. Examples of a variable breaker parameter
can be found in Nelson (1987) and Ruessink et al. (2003). (Both are implemented in SWAN.)
The constant value is 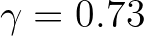 found as
the mean value of the data set of Battjes and Stive (1985).
found as
the mean value of the data set of Battjes and Stive (1985).
Nonlinear wave-wave interactions
The basic properties of wave-wave interactions were discovered during the fundamental research
of Phillips (1960) and Hasselmann (1960, 1962, 1963a,b). The physical meaning of the interactions is that
resonant sets of wave components exchange energy, redistributing energy over the spectrum. In deep
and intermediate water, four-wave interactions (so-called quadruplets) are important, whereas
in shallow water three-wave interactions (so-called triads) become important.
In deep water, quadruplet wave-wave interactions dominate the evolution of the spectrum. They transfer
wave energy from the spectral peak to lower frequencies (thus moving the peak frequency to lower values)
and to higher frequencies (where the energy is dissipated by whitecapping). In very shallow water, triad
wave-wave interactions transfer energy from lower frequencies to higher frequencies often resulting in
higher harmonics (Beji and Battjes, 1993). Low-frequency energy generation by triad wave-wave
interactions is also possible and is considered here as well.
A full computation of the quadruplet wave-wave interactions is extremely time consuming and not
convenient in an operational wave model. Nevertheless, SWAN has an option to compute the Boltzmann integral
in an exact manner. The approach is the exact method developed by Webb, Tracy and Resio (WRT)
(Resio et al., 2001). This algorithm was reprogrammed by Van Vledder, bearing the name XNL
(Van Vledder and Bottema, 2003). This method is also enable to capture the frequency shift and the spectral
shape changes as water depth decreases.
A number of techniques, based on parametric methods and approximations have been proposed to
improve computational speed of computing quadruplets (see Young and Van Vledder (1993) for a review). In SWAN,
the computations are carried out with the Discrete Interaction Approximation (DIA) of Hasselmann et al.
(1985). This DIA has been found to be quite successful in describing the essential features of a
developing wave spectrum; see Komen et al. (1994). For uni-directional waves, this approximation is not
valid. In fact, the quadruplet interaction coefficient for these waves is nearly zero. For finite-depth
applications, Hasselmann and Hasselmann (1981) have shown that for a JONSWAP-type spectrum the quadruplet
wave-wave interactions can be scaled with a simple expression.
In some cases, the DIA technique may not be accurate enough. In Hashimoto et al. (2002), it was
demonstrated that the accuracy of the DIA may be improved by increasing the number of quadruplet
configurations. They proposed a Multiple DIA with up to 6 wave number configurations.
In very shallow water, triad wave interactions become important for shoaling waves. It
transfers energy to higher and lower frequencies, resulting in super and sub harmonics
(Eldeberky, 1996; Herbers and Burton, 1997; Becq-Girard et al, 1999).
The energy transfer in this process can take place over relatively short distance and can
dramatically change single peaked spectra into multiple peaked spectra, which has frequently
been observed in the field (Arcilla et al., 1994) and in a number of laboratory
experiments with a bar-trough profile (Beji and Battjes, 1993) and a plane beach profile
(Nwogu, 1994).
A first attempt to describe triad wave-wave interactions in terms of a spectral energy source term was
made by Abreu et al. (1992). However, their expression is restricted to non-dispersive shallow water
waves and is therefore not suitable in many practical applications of wind waves. The breakthrough in the
development came with the work of Eldeberky and Battjes (1995) who transformed the amplitude spectrum of
the Boussinesq model of Madsen and Sørensen (1993) into an energy density formulation and who
parameterized the biphase of the triad on the basis of laboratory observations (Battjes and Beji, 1992;
Arcilla et al., 1994). Here, the quasi-Gaussian hypothesis is assumed which neglect the fourth-order
cumulant allowing to express the bispectrum in terms of second-order energy products and the biphase.
A discrete triad approximation (DTA) for collinear waves (i.e. directionally uncoupled) was subsequently
obtained by considering only the dominant self-self interactions. This model has been verified with flume
observations of long-crested, random waves breaking over a submerged bar (Beji and Battjes, 1993) and
over a barred beach (Arcilla et al., 1994). The model appeared to be fairly successful in describing
the essential features of the energy transfer from the primary peak of the spectrum to the super harmonics.
A slightly different version, the so-called Lumped Triad Approximation (LTA) was later derived by
Eldeberky (1996). This LTA technique is implemented in SWAN.
An alternative triad model is the Stochastic Parametric model based on Boussinesq
equations (SPB) model derived by Becq-Girard et al. (1999). Like the LTA, the SPB is
based on the Boussinesq-type equations of Madsen and Sørensen (1993). However, instead of fully neglecting
the fourth-order cumulants, these contributions are assumed to be proportional to the bispectrum
itself  the so-called closure hypothesis of Holloway (1980)
the so-called closure hypothesis of Holloway (1980)  by introducing an empirical
parameter
by introducing an empirical
parameter 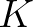 (see their Eq. 2.21). In effect, this represents a length scale over which the bispectrum, in the
absence of forcing, returns to zero. Unlike the LTA, the SPB model generates all possible (sum and difference)
interactions of the collinear waves.
(see their Eq. 2.21). In effect, this represents a length scale over which the bispectrum, in the
absence of forcing, returns to zero. Unlike the LTA, the SPB model generates all possible (sum and difference)
interactions of the collinear waves.
The SPB model is implemented in SWAN. However, practical applications demonstrated the lack of robustness
of this model. Therefore, an alternative to the SPB technique is proposed in SWAN called the Full Triad
Interaction Model (FTIM). Like the SPB, this model takes into account all possible collinear interactions
but assumes the quasi-Gaussian hypothesis, similar to the LTA.
Here, we use the same biphase parametrization of Eldeberky (1996).
Another development for the representation of triad interactions in SWAN is due to Booij et al. (2009),
called the Distributed Collinear Triad Approximation (DCTA). Its expression is similar to that of the
quadruplet wave-wave interaction while removing one component from the expression. In addition, the
associated scaling heuristically forces the spectral tail to converge to the equilibrium 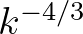 high-frequency tail at shallow water depths (
high-frequency tail at shallow water depths (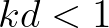 ).
In effect, DCTA accounts for both the initial generation of all sub and super harmonics and the transition to
a universal smooth tail.
).
In effect, DCTA accounts for both the initial generation of all sub and super harmonics and the transition to
a universal smooth tail.
The SWAN team 2024-09-09
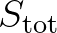 :
:
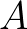 and
and 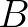 depend on wave frequency and direction, and wind speed and direction. The effects of
currents are accounted for by using the apparent local wind speed and direction. The expression
for the term
depend on wave frequency and direction, and wind speed and direction. The effects of
currents are accounted for by using the apparent local wind speed and direction. The expression
for the term 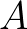 is due to Cavaleri and Malanotte-Rizzoli (1981) with a filter to avoid growth at frequencies
lower than the Pierson-Moskowitz frequency (Tolman, 1992a). Two optional expressions for the coefficient
is due to Cavaleri and Malanotte-Rizzoli (1981) with a filter to avoid growth at frequencies
lower than the Pierson-Moskowitz frequency (Tolman, 1992a). Two optional expressions for the coefficient
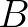 are used in the SWAN model. The first is taken from an early version of the WAM Cycle 3 model
(the WAMDI group, 1988). It is due to Snyder et al. (1981), rescaled in terms of friction velocity
are used in the SWAN model. The first is taken from an early version of the WAM Cycle 3 model
(the WAMDI group, 1988). It is due to Snyder et al. (1981), rescaled in terms of friction velocity
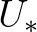 by Komen et al. (1984). The drag coefficient to relate
by Komen et al. (1984). The drag coefficient to relate 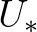 to the driving wind speed at 10 m elevation
to the driving wind speed at 10 m elevation
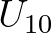 is taken from either Wu (1982) or Zijlema et al. (2012). The second expression for
is taken from either Wu (1982) or Zijlema et al. (2012). The second expression for 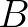 in SWAN is taken from the
WAM Cycle 4 model (Komen et al., 1994). It is due to Janssen (1991a) and it accounts
explicitly for the interaction between the wind and the waves by considering atmospheric boundary layer
effects and the roughness length of the sea surface. The corresponding set of equations is solved (as
in the WAM model) with the iterative procedure of Mastenbroek et al. (1993).
in SWAN is taken from the
WAM Cycle 4 model (Komen et al., 1994). It is due to Janssen (1991a) and it accounts
explicitly for the interaction between the wind and the waves by considering atmospheric boundary layer
effects and the roughness length of the sea surface. The corresponding set of equations is solved (as
in the WAM model) with the iterative procedure of Mastenbroek et al. (1993).
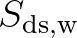 , bottom friction
, bottom friction 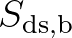 and depth-induced breaking
and depth-induced breaking 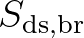 .
.
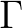 is a steepness dependent coefficient,
is a steepness dependent coefficient, 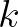 is wave number and
is wave number and
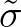 and
and 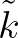 denote a mean frequency and a mean wave number, respectively (cf. the WAMDI group, 1988). Komen et al. (1984)
estimated the value of
denote a mean frequency and a mean wave number, respectively (cf. the WAMDI group, 1988). Komen et al. (1984)
estimated the value of 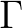 by closing the energy balance of the waves in fully developed conditions. This
implies that this value depends on the wind input formulation that is used. Since two expressions are used for the wind
input in SWAN, also two values for
by closing the energy balance of the waves in fully developed conditions. This
implies that this value depends on the wind input formulation that is used. Since two expressions are used for the wind
input in SWAN, also two values for 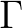 are used. The first is due to Komen et al. (1984), as in WAM Cycle 3.
The second expression is an adaptation of this expression based on Janssen (1991a), as in WAM Cycle 4
(see Janssen, 1991b; Günther et al., 1992). Young and Banner (1992) and Banner and Young (1994) have shown that
the results of closing the energy balance in this manner depend critically on the choice of a high-frequency cut-off
frequency above which a diagnostic spectral tail is used. In SWAN, this cut-off frequency is different from
the one used in the WAM model. Differences in the growth rates between the WAM model and SWAN are therefore to be
expected.
are used. The first is due to Komen et al. (1984), as in WAM Cycle 3.
The second expression is an adaptation of this expression based on Janssen (1991a), as in WAM Cycle 4
(see Janssen, 1991b; Günther et al., 1992). Young and Banner (1992) and Banner and Young (1994) have shown that
the results of closing the energy balance in this manner depend critically on the choice of a high-frequency cut-off
frequency above which a diagnostic spectral tail is used. In SWAN, this cut-off frequency is different from
the one used in the WAM model. Differences in the growth rates between the WAM model and SWAN are therefore to be
expected.
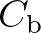 is a bottom friction coefficient. A large number of models has been proposed since the
pioneering paper of Putnam and Johnson (1949). Hasselmann et al. (1973) suggested to use an empirically
obtained constant. It seems to perform well in many different conditions as long as a suitable value is chosen
(typically different for swell and wind sea). A nonlinear formulation based on drag has been proposed by Hasselmann
and Collins (1968) which was later simplified by Collins (1972). More complicated, eddy viscosity models have been
developed by Madsen et al. (1988) and by Weber (1989, 1991a, 1991b). Considering the large variations in
bottom conditions in coastal areas (bottom material, bottom roughness length, ripple height, etc.), there
is no field data evidence to give preference to a particular friction model (Luo and Monbaliu, 1994). For
this reason, the simplest of each of these types of friction models has been implemented in SWAN: the
empirical JONSWAP model of Hasselmann et al. (1973), the drag law model of Collins (1972) and the
eddy-viscosity model of Madsen et al. (1988). The effect of a mean current on the wave energy dissipation
due to bottom friction is not taken into account in SWAN. The reasons for this are given by Tolman (1992b)
who argues that state-of-the-art expressions vary too widely in their effects to be acceptable. He found that
the error in finding a correct estimate of the bottom roughness length scale has a much larger impact on
the energy dissipation rate than the effect of a mean current.
is a bottom friction coefficient. A large number of models has been proposed since the
pioneering paper of Putnam and Johnson (1949). Hasselmann et al. (1973) suggested to use an empirically
obtained constant. It seems to perform well in many different conditions as long as a suitable value is chosen
(typically different for swell and wind sea). A nonlinear formulation based on drag has been proposed by Hasselmann
and Collins (1968) which was later simplified by Collins (1972). More complicated, eddy viscosity models have been
developed by Madsen et al. (1988) and by Weber (1989, 1991a, 1991b). Considering the large variations in
bottom conditions in coastal areas (bottom material, bottom roughness length, ripple height, etc.), there
is no field data evidence to give preference to a particular friction model (Luo and Monbaliu, 1994). For
this reason, the simplest of each of these types of friction models has been implemented in SWAN: the
empirical JONSWAP model of Hasselmann et al. (1973), the drag law model of Collins (1972) and the
eddy-viscosity model of Madsen et al. (1988). The effect of a mean current on the wave energy dissipation
due to bottom friction is not taken into account in SWAN. The reasons for this are given by Tolman (1992b)
who argues that state-of-the-art expressions vary too widely in their effects to be acceptable. He found that
the error in finding a correct estimate of the bottom roughness length scale has a much larger impact on
the energy dissipation rate than the effect of a mean current.
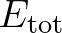 is the total wave energy and
is the total wave energy and
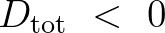 is the rate of dissipation of
the total energy due to wave breaking according to Battjes and Janssen (1978).
The value of
is the rate of dissipation of
the total energy due to wave breaking according to Battjes and Janssen (1978).
The value of 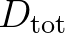 depends critically on the breaker parameter
depends critically on the breaker parameter
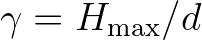 (in which
(in which 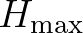 is the maximum possible individual wave height in the local water depth
is the maximum possible individual wave height in the local water depth 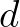 ).
In SWAN, both a constant value and a variable value are available. Examples of a variable breaker parameter
can be found in Nelson (1987) and Ruessink et al. (2003). (Both are implemented in SWAN.)
The constant value is
).
In SWAN, both a constant value and a variable value are available. Examples of a variable breaker parameter
can be found in Nelson (1987) and Ruessink et al. (2003). (Both are implemented in SWAN.)
The constant value is 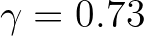 found as
the mean value of the data set of Battjes and Stive (1985).
found as
the mean value of the data set of Battjes and Stive (1985).
 the so-called closure hypothesis of Holloway (1980)
the so-called closure hypothesis of Holloway (1980)  by introducing an empirical
parameter
by introducing an empirical
parameter 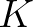 (see their Eq. 2.21). In effect, this represents a length scale over which the bispectrum, in the
absence of forcing, returns to zero. Unlike the LTA, the SPB model generates all possible (sum and difference)
interactions of the collinear waves.
(see their Eq. 2.21). In effect, this represents a length scale over which the bispectrum, in the
absence of forcing, returns to zero. Unlike the LTA, the SPB model generates all possible (sum and difference)
interactions of the collinear waves.
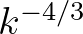 high-frequency tail at shallow water depths (
high-frequency tail at shallow water depths (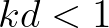 ).
In effect, DCTA accounts for both the initial generation of all sub and super harmonics and the transition to
a universal smooth tail.
).
In effect, DCTA accounts for both the initial generation of all sub and super harmonics and the transition to
a universal smooth tail.