Next: Dissipation of wave energy Up: Sources and sinks Previous: General concepts
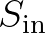 )
)
Wave growth by wind is described by
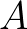 describes linear growth and
describes linear growth and 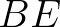 exponential growth. It should be noted that the SWAN model
is driven by the wind speed at 10m elevation
exponential growth. It should be noted that the SWAN model
is driven by the wind speed at 10m elevation 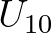 whereas it uses the friction velocity
whereas it uses the friction velocity
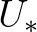 . For the WAM Cycle 3 formulation the transformation from
. For the WAM Cycle 3 formulation the transformation from 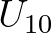 to
to 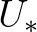 is obtained with
is obtained with
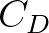 is the drag coefficient from Wu (1982):
is the drag coefficient from Wu (1982):
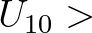 20 m/s, say).
Based on many authoritative studies it appears that the drag coefficient increases almost linearly with wind speed up to approximately
20 m/s, then levels off and decreases again at about 35 m/s to rather low values at 60 m/s wind speed.
We fitted a 2nd order polynomial to the data obtained from these studies, and this fit is given by
20 m/s, say).
Based on many authoritative studies it appears that the drag coefficient increases almost linearly with wind speed up to approximately
20 m/s, then levels off and decreases again at about 35 m/s to rather low values at 60 m/s wind speed.
We fitted a 2nd order polynomial to the data obtained from these studies, and this fit is given by
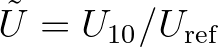 , and the reference wind speed
, and the reference wind speed 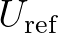 = 31.5 m/s is the speed at which the drag attains its maximum value
in this expression. These drag values are lower than in the expression of Wu (1982) by 10%
= 31.5 m/s is the speed at which the drag attains its maximum value
in this expression. These drag values are lower than in the expression of Wu (1982) by 10%  30% for high wind speeds
(15
30% for high wind speeds
(15
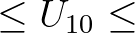 30 m/s) and over 30% for hurricane wind speeds (
30 m/s) and over 30% for hurricane wind speeds (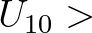 30 m/s). More details can be found in Zijlema et al. (2012).
Since version 41.01, the SWAN model employs the drag formulation as given by Eq. (2.36).
30 m/s). More details can be found in Zijlema et al. (2012).
Since version 41.01, the SWAN model employs the drag formulation as given by Eq. (2.36).
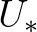 is an integral part of the source term.
is an integral part of the source term.
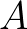 , the expression due to Cavaleri and Malanotte-Rizzoli (1981) is used with a
filter to eliminate wave growth at frequencies lower than the Pierson-Moskowitz frequency (Tolman,
1992a)2.1:
, the expression due to Cavaleri and Malanotte-Rizzoli (1981) is used with a
filter to eliminate wave growth at frequencies lower than the Pierson-Moskowitz frequency (Tolman,
1992a)2.1:
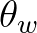 is the wind direction,
is the wind direction, 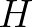 is the filter and
is the filter and
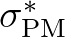 is the peak frequency of the
fully developed sea state according to Pierson and Moskowitz (1964) as reformulated in terms of friction velocity.
is the peak frequency of the
fully developed sea state according to Pierson and Moskowitz (1964) as reformulated in terms of friction velocity.
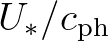 :
:
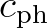 is the phase speed and
is the phase speed and 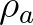 and
and 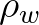 are the density of air and water, respectively. This
expression is also used in WAM Cycle 3 (the WAMDI group, 1988). The second expression is due to Janssen (1989,1991a).
It is based on a quasi-linear wind-wave theory and is given by
are the density of air and water, respectively. This
expression is also used in WAM Cycle 3 (the WAMDI group, 1988). The second expression is due to Janssen (1989,1991a).
It is based on a quasi-linear wind-wave theory and is given by
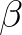 is the Miles constant. In the theory of Janssen (1991a), this constant is estimated from
the non-dimensional critical height
is the Miles constant. In the theory of Janssen (1991a), this constant is estimated from
the non-dimensional critical height 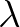 :
:
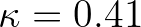 is the Von Karman constant and
is the Von Karman constant and 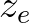 is the effective surface roughness.
If the non-dimensional critical height
is the effective surface roughness.
If the non-dimensional critical height 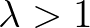 , the Miles constant
, the Miles constant 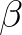 is set equal 0.
Janssen (1991a) assumes that the wind profile is given by
is set equal 0.
Janssen (1991a) assumes that the wind profile is given by
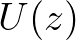 is the wind speed at height
is the wind speed at height 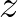 (10m in the SWAN model) above the mean water level,
(10m in the SWAN model) above the mean water level, 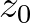 is
the roughness length. The effective roughness length
is
the roughness length. The effective roughness length 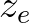 depends on the roughness length
depends on the roughness length 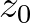 and the sea
state through the wave-induced stress
and the sea
state through the wave-induced stress 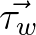 and the total surface stress
and the total surface stress
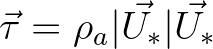 :
:
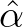 is a constant equal to 0.01. The
wave stress
is a constant equal to 0.01. The
wave stress 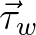 is given by
is given by
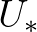 can be determined for a given wind speed
can be determined for a given wind speed 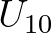 and a given wave spectrum
and a given wave spectrum
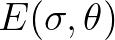 from the
above set of equations. In the SWAN model, the iterative procedure of Mastenbroek et al. (1993) is used.
This set of expressions (2.39) through (2.43) is also used in WAM Cycle 4 (Komen et al., 1994).
from the
above set of equations. In the SWAN model, the iterative procedure of Mastenbroek et al. (1993) is used.
This set of expressions (2.39) through (2.43) is also used in WAM Cycle 4 (Komen et al., 1994).
The SWAN team 2024-09-09