- 2.1
- In Eq. (10) of Tolman (1992a) the power of
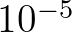 should be
should be 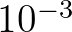 ; H. Tolman, personal
communication, 1995.
; H. Tolman, personal
communication, 1995.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- 2.2
- Collins (1972) contains
an error in the expression due to an erroneous Jacobian transformation. See page A-16 of Tolman (1990).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- 2.3
- The time evolution of wave action of a wave packet is naturally described as evolving along a trajectory (or ray) through the phase space
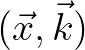 .
In this sense, the local wave number vector
.
In this sense, the local wave number vector 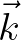 conjugates to the position
conjugates to the position  owing to the linear dispersion relation of water waves, assuming
a slowly varying medium in physical space (McDonald, 1988). The variables
owing to the linear dispersion relation of water waves, assuming
a slowly varying medium in physical space (McDonald, 1988). The variables  and
and 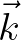 are called the canonical coordinates in phase space with the components of
are called the canonical coordinates in phase space with the components of  to be
the usual Cartesian coordinates
to be
the usual Cartesian coordinates 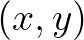 and the components of
and the components of 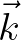 to be the conjugate momenta
to be the conjugate momenta 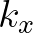 and
and 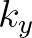 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- 2.4
- Unless otherwise stated, integrals are with infinite limits.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- 2.5
- Likewise, the marginal
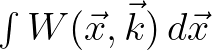 yields the distribution
yields the distribution
 described in spectral space.
described in spectral space.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- 2.6
- Strictly speaking, in the presence of the ambient current, the so-called action variable
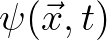 should be employed
instead of
should be employed
instead of
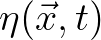 . This variable is characterized by its surface elevation
. This variable is characterized by its surface elevation
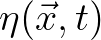 and surface potential
and surface potential
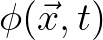 .
Without reproducing the rather involved definition of
.
Without reproducing the rather involved definition of 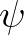 (see Akrish et al. (2020), their Eq. (2.2)),
we just keep the notion of
(see Akrish et al. (2020), their Eq. (2.2)),
we just keep the notion of 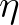 here as it is helpful to comprehend the rest of this section without further consequences.
here as it is helpful to comprehend the rest of this section without further consequences.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- 2.7
- A pseudo-differential operator is the inverse Fourier transform of the multiplication of
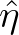 by a symbol (here
by a symbol (here 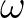 ) in Fourier space
and can be considered as a generalized differential operator.
This is evidenced by the fact that the Fourier transform of a pseudo-differential operator acting on a function living in physical space can be expressed as the Fourier multiplier operator
in Fourier space, that is,
given the pseudo-differential operator
) in Fourier space
and can be considered as a generalized differential operator.
This is evidenced by the fact that the Fourier transform of a pseudo-differential operator acting on a function living in physical space can be expressed as the Fourier multiplier operator
in Fourier space, that is,
given the pseudo-differential operator
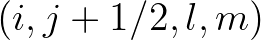 (or a special case, the derivative
(or a special case, the derivative
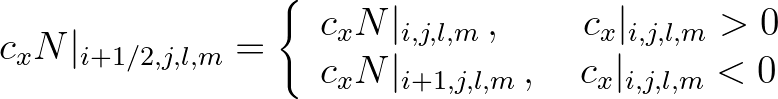 ) with symbol
) with symbol
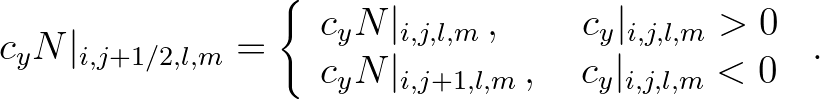 (or
(or 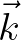 in the special case)
we have
in the special case)
we have
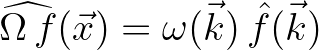 for any smooth compactly supported function
for any smooth compactly supported function 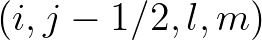 and its Fourier transform
and its Fourier transform
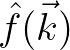 .
The use of pseudo-differential operators is of great importance in describing the dynamics of water waves and wave functions in quantum mechanics.
.
The use of pseudo-differential operators is of great importance in describing the dynamics of water waves and wave functions in quantum mechanics.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- 2.8
- We suppress the variable
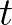 in the argument of
in the argument of 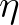 and other functions for the convenience of presentation.
and other functions for the convenience of presentation.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- 2.9
- If operators
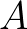 and
and 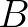 do not commute, that is,
do not commute, that is,
![$[A,B] \equiv AB - BA \neq0$](img748.png) , but they commute with their commutator,
, but they commute with their commutator,
![$[A,[A,B]] = [B,[A,B]] = 0$](img749.png) , then the BCH formula is given by
, then the BCH formula is given by
![$e^{A+B} = e^A\,e^B\,e^{-[A,B]/2}$](img750.png) . This is a commonly used formula in quantum mechanics.
. This is a commonly used formula in quantum mechanics.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- 2.10
- As a matter of fact, the cross correlations are due to the interaction with a medium that varies slowly in space.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- 2.11
- Wave refraction and Doppler shifting can be modelled explicitly through the term
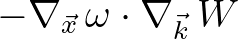 added to the left hand side of Eq. (2.225), as proposed in Smit et al. (2015a) using the local plane approximation, see pg. 1142 of their paper.
However, for a number of reasons that will become clear in Section 3.9, we will not do so here.
added to the left hand side of Eq. (2.225), as proposed in Smit et al. (2015a) using the local plane approximation, see pg. 1142 of their paper.
However, for a number of reasons that will become clear in Section 3.9, we will not do so here.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- 3.1
- In the present context, we consider the discretization of the divergence operator
applied to the energy flux. See Zijlema (2021) for details.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- 3.2
- Waves can be blocked by the current at a relative high frequency.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- 3.3
- Although in SWAN the number of sweeps
equals 4 and is hard-coded.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- 3.4
- The equivalent situation for such an equation is to have eigenvalues
of very different magnitudes.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- 3.5
- It is
noted here that the effective
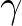 used in SWAN is not equivalent to that of
WAM: the former is a factor
used in SWAN is not equivalent to that of
WAM: the former is a factor 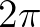 larger.
larger.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- 3.6
- The Lipschitz criterion is well known in the field of semi-Lagrangian schemes and its
interpretation is that trajectories do not cross each other during one Lagrangian time step. See e.g. Smolarkiewicz and Pudykiewicz (1992) and Lin and Rood (1996).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- 3.7
- The spatial turning rate is the change in wave direction per unit forward distance
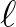 that is travelled by the wave energy in a
time interval
that is travelled by the wave energy in a
time interval 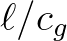 , and thus represents the curvature of the wave ray. This is equivalent to
, and thus represents the curvature of the wave ray. This is equivalent to 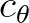 , which is the turning rate of the wave direction per unit time.
, which is the turning rate of the wave direction per unit time.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- 3.8
- According to the Snel's law a wave direction with respect to the normal of a coastline within a directional bin
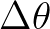 can not turn more than
can not turn more than 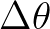 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- 7.1
- Available from http://www-unix.mcs.anl.gov/mpi/mpich.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
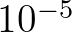 should be
should be 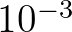 ; H. Tolman, personal
communication, 1995.
; H. Tolman, personal
communication, 1995.
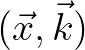 .
In this sense, the local wave number vector
.
In this sense, the local wave number vector 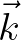 conjugates to the position
conjugates to the position  owing to the linear dispersion relation of water waves, assuming
a slowly varying medium in physical space (McDonald, 1988). The variables
owing to the linear dispersion relation of water waves, assuming
a slowly varying medium in physical space (McDonald, 1988). The variables  and
and 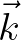 are called the canonical coordinates in phase space with the components of
are called the canonical coordinates in phase space with the components of  to be
the usual Cartesian coordinates
to be
the usual Cartesian coordinates 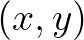 and the components of
and the components of 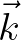 to be the conjugate momenta
to be the conjugate momenta 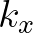 and
and 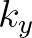 .
.
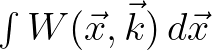 yields the distribution
yields the distribution
 described in spectral space.
described in spectral space.
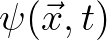 should be employed
instead of
should be employed
instead of
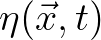 . This variable is characterized by its surface elevation
. This variable is characterized by its surface elevation
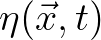 and surface potential
and surface potential
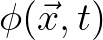 .
Without reproducing the rather involved definition of
.
Without reproducing the rather involved definition of 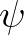 (see Akrish et al. (2020), their Eq. (2.2)),
we just keep the notion of
(see Akrish et al. (2020), their Eq. (2.2)),
we just keep the notion of 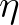 here as it is helpful to comprehend the rest of this section without further consequences.
here as it is helpful to comprehend the rest of this section without further consequences.
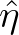 by a symbol (here
by a symbol (here 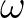 ) in Fourier space
and can be considered as a generalized differential operator.
This is evidenced by the fact that the Fourier transform of a pseudo-differential operator acting on a function living in physical space can be expressed as the Fourier multiplier operator
in Fourier space, that is,
given the pseudo-differential operator
) in Fourier space
and can be considered as a generalized differential operator.
This is evidenced by the fact that the Fourier transform of a pseudo-differential operator acting on a function living in physical space can be expressed as the Fourier multiplier operator
in Fourier space, that is,
given the pseudo-differential operator
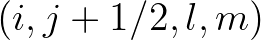 (or a special case, the derivative
(or a special case, the derivative
 ) with symbol
) with symbol
 (or
(or  in the special case)
we have
in the special case)
we have
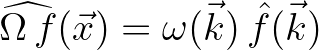 for any smooth compactly supported function
for any smooth compactly supported function 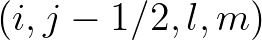 and its Fourier transform
and its Fourier transform
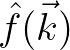 .
The use of pseudo-differential operators is of great importance in describing the dynamics of water waves and wave functions in quantum mechanics.
.
The use of pseudo-differential operators is of great importance in describing the dynamics of water waves and wave functions in quantum mechanics.
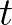 in the argument of
in the argument of 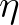 and other functions for the convenience of presentation.
and other functions for the convenience of presentation.
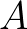 and
and 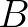 do not commute, that is,
do not commute, that is,
![$[A,B] \equiv AB - BA \neq0$](img748.png) , but they commute with their commutator,
, but they commute with their commutator,
![$[A,[A,B]] = [B,[A,B]] = 0$](img749.png) , then the BCH formula is given by
, then the BCH formula is given by
![$e^{A+B} = e^A\,e^B\,e^{-[A,B]/2}$](img750.png) . This is a commonly used formula in quantum mechanics.
. This is a commonly used formula in quantum mechanics.
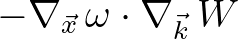 added to the left hand side of Eq. (2.225), as proposed in Smit et al. (2015a) using the local plane approximation, see pg. 1142 of their paper.
However, for a number of reasons that will become clear in Section 3.9, we will not do so here.
added to the left hand side of Eq. (2.225), as proposed in Smit et al. (2015a) using the local plane approximation, see pg. 1142 of their paper.
However, for a number of reasons that will become clear in Section 3.9, we will not do so here.
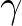 used in SWAN is not equivalent to that of
WAM: the former is a factor
used in SWAN is not equivalent to that of
WAM: the former is a factor 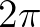 larger.
larger.
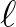 that is travelled by the wave energy in a
time interval
that is travelled by the wave energy in a
time interval 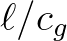 , and thus represents the curvature of the wave ray. This is equivalent to
, and thus represents the curvature of the wave ray. This is equivalent to 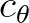 , which is the turning rate of the wave direction per unit time.
, which is the turning rate of the wave direction per unit time.
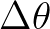 can not turn more than
can not turn more than 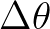 .
.