Next: Nonlinear wave-wave interactions () Up: Sources and sinks Previous: Input by wind ()
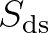 )
)
Whitecapping: Komen et al. (1984) formulation
The processes of whitecapping in the SWAN model is represented by the pulse-based model of
Hasselmann (1974). Reformulated in terms of wave number (rather than frequency) so as to be
applicable in finite water depth (cf. the WAMDI group, 1988), this expression is:
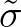 and
and 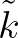 denote the mean frequency and the mean wave number,
respectively, and the coefficient
denote the mean frequency and the mean wave number,
respectively, and the coefficient 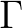 depends on the overall wave steepness. This steepness dependent
coefficient, as given by the WAMDI group (1988), has been adapted by Günther et al. (1992) based on
Janssen (1991a) (see also (Janssen, 1991b)):
depends on the overall wave steepness. This steepness dependent
coefficient, as given by the WAMDI group (1988), has been adapted by Günther et al. (1992) based on
Janssen (1991a) (see also (Janssen, 1991b)):
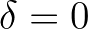 the expression of
the expression of 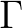 reduces to the expression as used by the WAMDI group (1988). The
coefficients
reduces to the expression as used by the WAMDI group (1988). The
coefficients 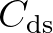 ,
, 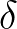 and
and 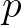 are tunable coefficients,
are tunable coefficients, 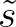 is the overall wave
steepness,
is the overall wave
steepness,
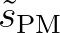 is the value of
is the value of 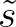 for the Pierson-Moskowitz
spectrum (1964):
for the Pierson-Moskowitz
spectrum (1964):
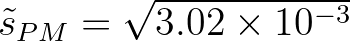 . The overall wave steepness
. The overall wave steepness 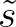 is defined as
is defined as
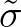 , the mean wave number
, the mean wave number 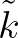 and the total wave energy
and the total wave energy
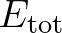 are defined as (cf. the WAMDI group, 1988):
are defined as (cf. the WAMDI group, 1988):
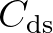 and
and 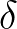 and exponent
and exponent 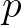 in this model have been obtained by
Komen et al. (1984) and Janssen (1992) by closing the energy balance of the waves in idealized wave growth conditions
(both for growing and fully developed wind seas) for deep water. This implies that coefficients in the steepness dependent
coefficient
in this model have been obtained by
Komen et al. (1984) and Janssen (1992) by closing the energy balance of the waves in idealized wave growth conditions
(both for growing and fully developed wind seas) for deep water. This implies that coefficients in the steepness dependent
coefficient 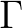 depend on the wind input formulation that is used. Since two different wind input formulations are
used in the SWAN model, two sets of coefficients are used. For the wind input of Komen et al. (1984; corresponding to WAM
Cycle 3; the WAMDI group, 1988):
depend on the wind input formulation that is used. Since two different wind input formulations are
used in the SWAN model, two sets of coefficients are used. For the wind input of Komen et al. (1984; corresponding to WAM
Cycle 3; the WAMDI group, 1988):
 ,
, 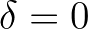 and
and 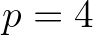 . Janssen (1992) and also
Günther et al. (1992) obtained (assuming
. Janssen (1992) and also
Günther et al. (1992) obtained (assuming 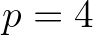 )
)
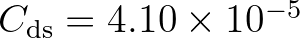 and
and 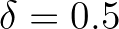 (as used in the WAM
Cycle 4; Komen et al., 1994).
(as used in the WAM
Cycle 4; Komen et al., 1994).
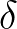 from 0 to 1 leads to an improved prediction of the wave energy at lower frequencies.
Because of this,
from 0 to 1 leads to an improved prediction of the wave energy at lower frequencies.
Because of this, 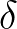 is set to 1 as default since version 40.91A.
However, it should be mentioned that adapting
is set to 1 as default since version 40.91A.
However, it should be mentioned that adapting
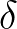 without retuning
without retuning
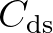 may lead to exceedence of the theoretical limits on wave height proposed by
Pierson and Moskowitz (1964).
may lead to exceedence of the theoretical limits on wave height proposed by
Pierson and Moskowitz (1964).
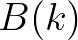 is the azimuthal-integrated spectral saturation, which is positively correlated with
the probability of wave group-induced breaking. It is calculated from frequency space variables as follows
is the azimuthal-integrated spectral saturation, which is positively correlated with
the probability of wave group-induced breaking. It is calculated from frequency space variables as follows
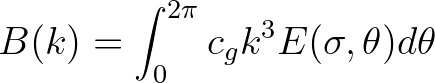 (2.51)
(2.51)
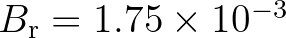 is a threshold saturation level. The proportionality coefficient is set to
is a threshold saturation level. The proportionality coefficient is set to
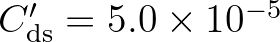 . When
. When
 , waves break and the exponent
, waves break and the exponent  is set equal
to a calibration parameter
is set equal
to a calibration parameter  . For
. For
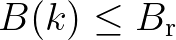 there is no breaking, but some residual dissipation proved
necessary. This is obtained by setting
there is no breaking, but some residual dissipation proved
necessary. This is obtained by setting 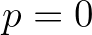 . A smooth transition between these two situations is achieved by
(Alves and Banner, 2003)
. A smooth transition between these two situations is achieved by
(Alves and Banner, 2003)
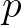 is simply set to
is simply set to 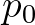 (see below).
(see below).
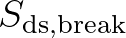 is the contribution by breaking waves (2.50), and
is the contribution by breaking waves (2.50), and
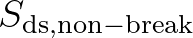 dissipation
by means other than breaking (e.g. turbulence). The changeover between the two modes is made with a smooth transition
function
dissipation
by means other than breaking (e.g. turbulence). The changeover between the two modes is made with a smooth transition
function 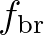 similar to (2.52):
similar to (2.52):
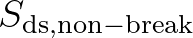 , to provide general
background dissipation of non-breaking waves. For this component, the parameter settings of Komen et al. (1984)
are applied.
, to provide general
background dissipation of non-breaking waves. For this component, the parameter settings of Komen et al. (1984)
are applied.
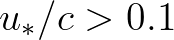 say, the wind-induced growth rate of waves depends quadratically on
say, the wind-induced growth rate of waves depends quadratically on
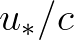 (e.g. Plant 1982), whereas for weaker forcing,
(e.g. Plant 1982), whereas for weaker forcing, 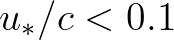 say, the growth rate depends linearly on
say, the growth rate depends linearly on 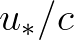 (Snyder et al., 1981). Yan (1987) proposes an analytical fit through these two ranges of the form:
(Snyder et al., 1981). Yan (1987) proposes an analytical fit through these two ranges of the form:
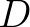 ,
,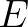 ,
,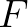 and
and 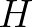 are coefficients of the fit. Yan imposed two constraints:
are coefficients of the fit. Yan imposed two constraints:
 and
and
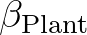 are the growth rates proposed by Snyder et al. (1981) and Plant (1982), respectively.
Application of Eqs. (2.56) and (2.57) led us to parameter values of
are the growth rates proposed by Snyder et al. (1981) and Plant (1982), respectively.
Application of Eqs. (2.56) and (2.57) led us to parameter values of
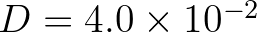 ,
,
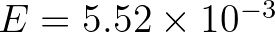 ,
,
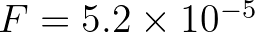 and
and
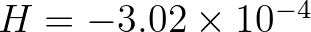 , which are somewhat different from those proposed by Yan (1987). We found that our parameter values produce better
fetch-limited simulation results in the Pierson and Moskowitz (1964) fetch range thant the original values of Yan (1987).
, which are somewhat different from those proposed by Yan (1987). We found that our parameter values produce better
fetch-limited simulation results in the Pierson and Moskowitz (1964) fetch range thant the original values of Yan (1987).
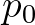 in Eqs. (2.50) and (2.52) is made by requiring that the source terms of whitecapping
(Eq. 2.50) and wind input (Eq. 2.55) have equal scaling in frequency, after Resio et al. (2004). This leads to a value of
in Eqs. (2.50) and (2.52) is made by requiring that the source terms of whitecapping
(Eq. 2.50) and wind input (Eq. 2.55) have equal scaling in frequency, after Resio et al. (2004). This leads to a value of
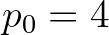 for strong wind forcing (
for strong wind forcing (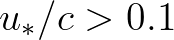 ) and
) and 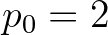 for weaker forcing (
for weaker forcing (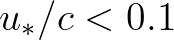 ). A smooth transition between these two limits,
centred around
). A smooth transition between these two limits,
centred around 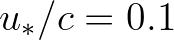 , is achieved by the expression
, is achieved by the expression
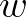 is a scaling parameter for which a value of
is a scaling parameter for which a value of 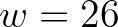 is used in SWAN. In shallow water, under strong wind forcing (
is used in SWAN. In shallow water, under strong wind forcing (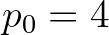 ), this
scaling condition requires the additional dimensionless factor
), this
scaling condition requires the additional dimensionless factor
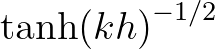 in Eq. (2.50), where
in Eq. (2.50), where 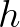 is the water depth.
is the water depth.
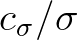 (2.13):
(2.13):
![$\displaystyle S_{\rm wc,curr} (\sigma,\theta) = -C''_{\rm ds} \max \left [ \fra...
...ma}, 0 \right ] \,\left( \frac{B(k)}{B_{\rm r}} \right)^{p/2} E(\sigma,\theta)
$](img227.png) (2.59)
(2.59)
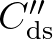 = 0.8. The remaining parameters are given by
Van der Westhuysen (2007), namely
= 0.8. The remaining parameters are given by
Van der Westhuysen (2007), namely
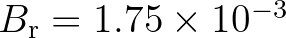 and
and 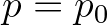 according to (2.58).
according to (2.58).
 (WW3) starting in 2010, and this
implementation was documented in Zieger et al. (2015). Since 2010, developments in the two models have largely
paralleled each other, insofar as most notable improvements are implemented in both models. As such, the documentation for WW3
(public release versions 4 or 5) is largely adequate documentation of significant changes to the source terms in SWAN since
the publication of Rogers et al. (2012), and do not need to be repeated here. We point out three notable exceptions to
this.
(WW3) starting in 2010, and this
implementation was documented in Zieger et al. (2015). Since 2010, developments in the two models have largely
paralleled each other, insofar as most notable improvements are implemented in both models. As such, the documentation for WW3
(public release versions 4 or 5) is largely adequate documentation of significant changes to the source terms in SWAN since
the publication of Rogers et al. (2012), and do not need to be repeated here. We point out three notable exceptions to
this.
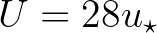 , following Komen et al. (1984), has been replaced with
, following Komen et al. (1984), has been replaced with
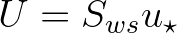 , where
, where 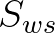 is a free parameter. Use of
is a free parameter. Use of 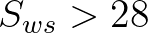 (we use
(we use 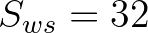 )
yields significant improvements to the tail level, correcting overprediction mean square slope. This necessitates
tuning of the
)
yields significant improvements to the tail level, correcting overprediction mean square slope. This necessitates
tuning of the 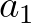 and
and 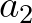 coefficients. Settings are suggested in the SWAN User Manual. At time of writing, this
feature has not yet been ported to WW3.
coefficients. Settings are suggested in the SWAN User Manual. At time of writing, this
feature has not yet been ported to WW3.
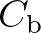 is a bottom friction coefficient that generally depends on the bottom orbital motion
represented by
is a bottom friction coefficient that generally depends on the bottom orbital motion
represented by 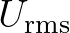 :
:
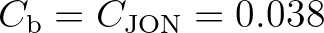 m
m s
s which is in
agreement with the JONSWAP result for swell dissipation. However, Bouws and Komen (1983) suggest a
value of
which is in
agreement with the JONSWAP result for swell dissipation. However, Bouws and Komen (1983) suggest a
value of
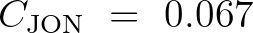 m
m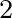 s
s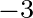 for depth-limited wind-sea conditions in the North Sea. This value is derived
from revisiting the energy balance equation employing an alternative deep water dissipation.
Recently, in Zijlema et al. (2012) it was found that a unified value of
for depth-limited wind-sea conditions in the North Sea. This value is derived
from revisiting the energy balance equation employing an alternative deep water dissipation.
Recently, in Zijlema et al. (2012) it was found that a unified value of 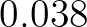 m
m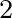 s
s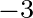 can be used if the
second order polyomial fit for wind drag of Eq. (2.36) is employed.
So, in SWAN 41.01 this is default irrespective of swell and wind-sea conditions.
can be used if the
second order polyomial fit for wind drag of Eq. (2.36) is employed.
So, in SWAN 41.01 this is default irrespective of swell and wind-sea conditions.
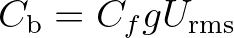 with
with 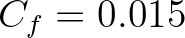 (Collins, 1972)2.2.
(Collins, 1972)2.2.
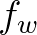 is a non-dimensional friction factor estimated by using the formulation of Jonsson (1966) cf.
Madsen et al. (1988):
is a non-dimensional friction factor estimated by using the formulation of Jonsson (1966) cf.
Madsen et al. (1988):
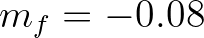 (Jonsson and Carlsen, 1976) and
(Jonsson and Carlsen, 1976) and 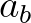 is a representative near-bottom excursion
amplitude:
is a representative near-bottom excursion
amplitude:
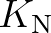 is the bottom roughness length scale. For values of
is the bottom roughness length scale. For values of 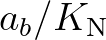 smaller than 1.57 the
friction factor
smaller than 1.57 the
friction factor 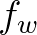 is 0.30 (Jonsson, 1980).
is 0.30 (Jonsson, 1980).
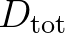 is expressed as
is expressed as
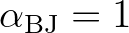 in SWAN,
in SWAN, 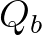 is the fraction of breaking waves determined by
is the fraction of breaking waves determined by
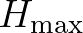 is the maximum wave height that can exist at the given depth and
is the maximum wave height that can exist at the given depth and
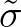 is a mean frequency defined as
is a mean frequency defined as
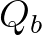 ) is determined in SWAN with
) is determined in SWAN with
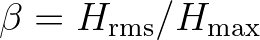 . Furthermore, for
. Furthermore, for
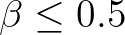 ,
, 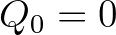 and for
and for
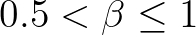 ,
,
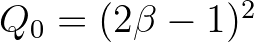 .
.
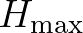 is determined in SWAN with
is determined in SWAN with
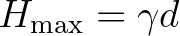 , in which
, in which 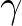 is the breaker parameter
and
is the breaker parameter
and 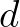 is the total water depth (including the wave-induced set-up if computed by SWAN). In the literature,
this breaker parameter
is the total water depth (including the wave-induced set-up if computed by SWAN). In the literature,
this breaker parameter 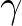 is often a constant or it is expressed as a function of bottom slope or incident
wave steepness (see e.g., Galvin, 1972; Battjes and Janssen, 1978; Battjes and Stive, 1985; Arcilla and
Lemos, 1990; Kaminsky and Kraus, 1993; Nelson, 1987, 1994).
In the publication of Battjes and Janssen (1978) in which the dissipation model is described, a constant
breaker parameter, based on Miche's criterion, of
is often a constant or it is expressed as a function of bottom slope or incident
wave steepness (see e.g., Galvin, 1972; Battjes and Janssen, 1978; Battjes and Stive, 1985; Arcilla and
Lemos, 1990; Kaminsky and Kraus, 1993; Nelson, 1987, 1994).
In the publication of Battjes and Janssen (1978) in which the dissipation model is described, a constant
breaker parameter, based on Miche's criterion, of 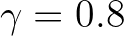 was used. Battjes and Stive (1985) re-analyzed
wave data of a number of laboratory and field experiments and found values for the breaker parameter
varying between 0.6 and 0.83 for different types of bathymetry (plane, bar-trough and bar) with an average
of 0.73. From a compilation of a large number of experiments Kaminsky and Kraus (1993) have found
breaker parameters in the range of 0.6 to 1.59 with an average of 0.79.
was used. Battjes and Stive (1985) re-analyzed
wave data of a number of laboratory and field experiments and found values for the breaker parameter
varying between 0.6 and 0.83 for different types of bathymetry (plane, bar-trough and bar) with an average
of 0.73. From a compilation of a large number of experiments Kaminsky and Kraus (1993) have found
breaker parameters in the range of 0.6 to 1.59 with an average of 0.79.
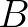 is a proportionality coefficient and
is a proportionality coefficient and 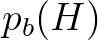 is the probability density function of breaking
waves times the fraction of breakers,
is the probability density function of breaking
waves times the fraction of breakers, 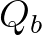 . Based on field observations, the wave heights in the surf zone
are assumed to remain Rayleigh distributed, even after breaking. This implies that all waves will break, not
only the highest as assumed by Battjes and Janssen (1978). The function
. Based on field observations, the wave heights in the surf zone
are assumed to remain Rayleigh distributed, even after breaking. This implies that all waves will break, not
only the highest as assumed by Battjes and Janssen (1978). The function 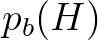 is obtained by multiplying
the Rayleigh wave height probability density function
is obtained by multiplying
the Rayleigh wave height probability density function 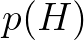 , given by
, given by
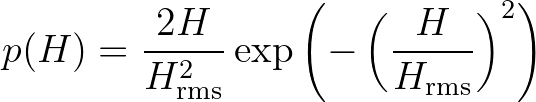 (2.71)
(2.71)
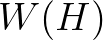 defined so that
defined so that
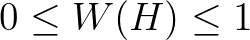 , to yield
, to yield
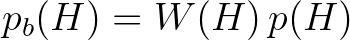 (2.72)
(2.72)
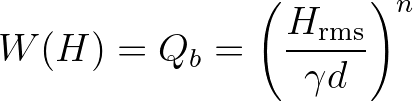 (2.73)
(2.73)
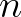 (=4) and a breaker index
(=4) and a breaker index 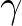 (not to be confused with the Battjes and Janssen breaker index!).
The integral in expression (2.70) can then be simplified, as follows
(not to be confused with the Battjes and Janssen breaker index!).
The integral in expression (2.70) can then be simplified, as follows
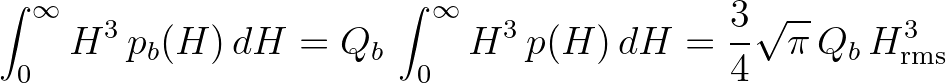 (2.74)
(2.74)
The SWAN team 2024-09-09