Next: Spectral action balance equation Up: Propagation of wave energy Previous: Propagation of wave energy
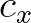 ,
, 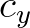 are the propagation velocities of wave energy in spatial
are the propagation velocities of wave energy in spatial 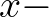 ,
, 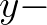 space,
space, 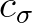 and
and 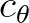 are the propagation velocities in spectral space
are the propagation velocities in spectral space 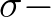 ,
, 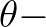 space,
space,
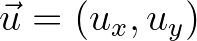 is the ambient current,
is the ambient current, 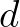 is the water depth,
is the water depth, 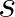 is the space co-ordinate
in the wave propagation direction of
is the space co-ordinate
in the wave propagation direction of 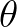 and
and 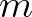 is a co-ordinate perpendicular to
is a co-ordinate perpendicular to 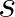 .
The expression for
.
The expression for 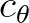 is presented here without diffraction effects. These are treated separately in Section 2.5.4.
is presented here without diffraction effects. These are treated separately in Section 2.5.4.
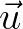 is assumed to be uniform with respect to the vertical co-ordinate.
In addition, the operator
is assumed to be uniform with respect to the vertical co-ordinate.
In addition, the operator 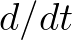 denotes the total derivative along a spatial path of energy propagation, and is defined as
denotes the total derivative along a spatial path of energy propagation, and is defined as
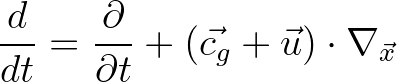 (2.15)
(2.15)
The SWAN team 2024-09-09