Next: Sources and sinks Up: Propagation of wave energy Previous: Wave kinematics
All information about the
sea surface is contained in the wave variance spectrum or energy density
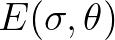 ,
distributing wave energy over (radian) frequencies
,
distributing wave energy over (radian) frequencies 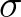 (as observed in a frame of
reference moving with current velocity) and propagation directions
(as observed in a frame of
reference moving with current velocity) and propagation directions 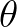 (the direction
normal to the wave crest of each spectral component).
(the direction
normal to the wave crest of each spectral component).
Usually, wave models determine the
evolution of the action density
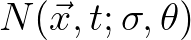 in space
in space  and
time
and
time 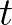 . The action density is defined as
. The action density is defined as 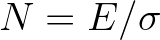 and is conserved during propagation along its wave characteristic
in the presence of ambient current, whereas energy density
and is conserved during propagation along its wave characteristic
in the presence of ambient current, whereas energy density 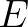 is not (Whitman, 1974). Wave action is said to be
adiabatic invariant.
is not (Whitman, 1974). Wave action is said to be
adiabatic invariant.
The rate of change of the action density 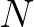 at a single point in space
at a single point in space
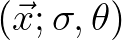 is governed by the action balance equation,
which reads (e.g., Mei, 1983; Komen et al., 1994)
is governed by the action balance equation,
which reads (e.g., Mei, 1983; Komen et al., 1994)
 -space, including wave shoaling, with
the group velocity
-space, including wave shoaling, with
the group velocity
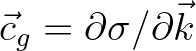 following from the
dispersion relation
following from the
dispersion relation
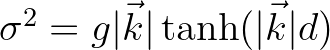 . The third term represents the effect of
shifting of the radian frequency due to variations in depth and mean currents. The fourth
term represents depth-induced and current-induced refraction. The quantities
. The third term represents the effect of
shifting of the radian frequency due to variations in depth and mean currents. The fourth
term represents depth-induced and current-induced refraction. The quantities 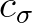 and
and
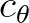 are the propagation velocities in spectral space
are the propagation velocities in spectral space
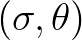 .
Notice that the second, third and fourth terms are divergence terms representing the amount of flux entering or leaving a point, and hence,
they act as source (negative divergence, i.e. flux entering a point) or sink (positive divergence, i.e. flux leaving a point) terms.
The right hand side contains
.
Notice that the second, third and fourth terms are divergence terms representing the amount of flux entering or leaving a point, and hence,
they act as source (negative divergence, i.e. flux entering a point) or sink (positive divergence, i.e. flux leaving a point) terms.
The right hand side contains 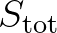 , which is the non-conservative source/sink term that
represents all physical processes which generate, dissipate, or redistribute wave energy at a point.
They are defined for energy density
, which is the non-conservative source/sink term that
represents all physical processes which generate, dissipate, or redistribute wave energy at a point.
They are defined for energy density
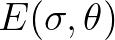 (i.e. not wave action). Details are given in Section 2.3.
(i.e. not wave action). Details are given in Section 2.3.
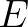 (being a transported quantity) with a transport velocity
(being a transported quantity) with a transport velocity 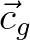 . The underlying
reason is that the group velocity is generally not divergence free. Instead, we rewrite Eq. (2.17) as
follows
. The underlying
reason is that the group velocity is generally not divergence free. Instead, we rewrite Eq. (2.17) as
follows
 (2.18)
(2.18)
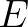 along the wave ray with velocity
along the wave ray with velocity 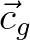 and the third term can be considered as a source or sink term with
respect to energy density
and the third term can be considered as a source or sink term with
respect to energy density 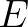 ; this density can be created (shoaling) or destroyed (de-shoaling) along the wave ray. This is due to
the change in the group velocity along this ray. The correct interpretation of the second term of Eq. (2.17) is the
divergence of the energy flux
; this density can be created (shoaling) or destroyed (de-shoaling) along the wave ray. This is due to
the change in the group velocity along this ray. The correct interpretation of the second term of Eq. (2.17) is the
divergence of the energy flux 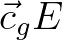 , i.e. the net energy flux per unit square (it measures the flux source or sink at a point).
The space discretization, as will be described in Section 3.2.1, is based on this interpretation.
, i.e. the net energy flux per unit square (it measures the flux source or sink at a point).
The space discretization, as will be described in Section 3.2.1, is based on this interpretation.
 with respect to longitude
with respect to longitude 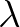 and latitude
and latitude 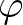 .
Note that
.
Note that 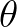 is the wave direction taken counterclockwise from geographic East. The propagation
velocities are reformulated as follows. On a sphere, we have
is the wave direction taken counterclockwise from geographic East. The propagation
velocities are reformulated as follows. On a sphere, we have
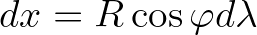 |
(2.21) | ||
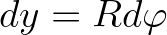 |
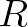 the radius of the earth. The propagation velocities in geographic space are then given by
the radius of the earth. The propagation velocities in geographic space are then given by
![$\displaystyle \frac{d\lambda}{dt} = c_\lambda = \frac{1}{R\cos \varphi} \left [...
...igma \vert\vec{k}\vert \cos \theta}{{\vert\vec{k}\vert}^2} + u_\lambda \right ]$](img95.png) |
(2.22) | ||
![$\displaystyle \frac{d\varphi}{dt} = c_\varphi = \frac{1}{R} \left [ \frac{1}{2}...
...igma \vert\vec{k}\vert \sin \theta}{{\vert\vec{k}\vert}^2} + u_\varphi \right ]$](img96.png) |
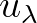 and
and 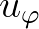 the ambient currents in longitude and latitude direction, respectively.
The propagation velocity in
the ambient currents in longitude and latitude direction, respectively.
The propagation velocity in 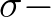 space remain unchanged. To rewrite the propagation velocity
space remain unchanged. To rewrite the propagation velocity
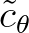 in terms of
spherical co-ordinates, we use the so-called Clairaut's equation that states that on any geodesic, the following expression
holds:
in terms of
spherical co-ordinates, we use the so-called Clairaut's equation that states that on any geodesic, the following expression
holds:
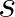 in wave direction gives
in wave direction gives
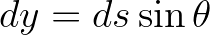 , we have
, we have
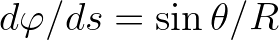 . Substitution into Eq. (2.24) and using
. Substitution into Eq. (2.24) and using
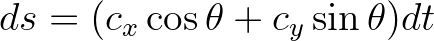 yields
yields
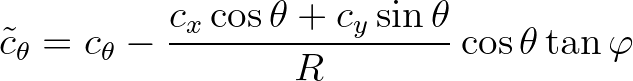 (2.26)
(2.26)
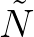 is related to the action density
is related to the action density 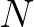 in a local Cartesian frame
in a local Cartesian frame 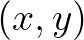 through
through
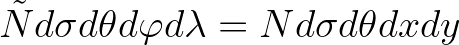 , or
, or
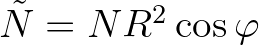 .
Substitution into (2.20) yields:
.
Substitution into (2.20) yields:
The SWAN team 2024-09-09