Next: Note on the choice Up: Discretization Previous: Discretization
Since the unknown 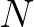 and the propagation velocities are only given in points
and the propagation velocities are only given in points 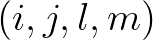 ,
further approximation is needed. A first order upwind scheme
in geographical space may be employed, since it is fully
monotone, i.e. it can not to give rise to spurious oscillations.
A disadvantage of this scheme is that it is numerically
diffusive, which naturally degrades the accuracy of the model.
This numerical diffusion is caused by gradients of wave action across geographic space, e.g. due to refraction by bathymetry or currents,
which is often small in coastal areas. So the wave energy field can be considered as smooth.
However, in
the current SWAN version, two alternatives to this scheme are implemented, namely the second
order SORDUP and Stelling/Leendertse schemes. These schemes produce far less numerical diffusion and are appropriate
for ocean and shelf sea (regional) applications.
,
further approximation is needed. A first order upwind scheme
in geographical space may be employed, since it is fully
monotone, i.e. it can not to give rise to spurious oscillations.
A disadvantage of this scheme is that it is numerically
diffusive, which naturally degrades the accuracy of the model.
This numerical diffusion is caused by gradients of wave action across geographic space, e.g. due to refraction by bathymetry or currents,
which is often small in coastal areas. So the wave energy field can be considered as smooth.
However, in
the current SWAN version, two alternatives to this scheme are implemented, namely the second
order SORDUP and Stelling/Leendertse schemes. These schemes produce far less numerical diffusion and are appropriate
for ocean and shelf sea (regional) applications.
First order upwind scheme; BSBT
The fluxes 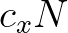 at
at 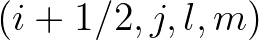 and
and 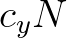 at
at 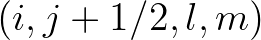 are approximated with an upwind scheme as follows
are approximated with an upwind scheme as follows
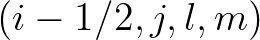 and
and 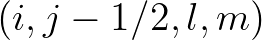 are obtained from (3.3) and (3.4),
respectively, by decreasing the indices by 1 in appropriate manner. According to the solution algorithm,
to be explained later in Section 3.3, both fluxes
at
are obtained from (3.3) and (3.4),
respectively, by decreasing the indices by 1 in appropriate manner. According to the solution algorithm,
to be explained later in Section 3.3, both fluxes
at 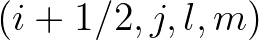 and
and 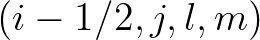 acts together with the same sign of
acts together with the same sign of 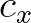 (either positive or negative).
Note that the flux
(either positive or negative).
Note that the flux 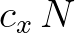 is considered as a whole quantity, and the propgation velocity
is considered as a whole quantity, and the propgation velocity 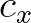 is taken in its
points of definition3.1.
The same holds for the fluxes at
is taken in its
points of definition3.1.
The same holds for the fluxes at 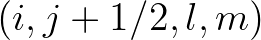 and
and 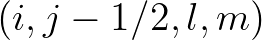 operating together with the same sign
of
operating together with the same sign
of 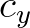 . These updates take place by ordering the grid points such that points solved later have no influence
on the previous grid points. This ordering and the associated updates are carried out, for instance, during the
first sweep if
. These updates take place by ordering the grid points such that points solved later have no influence
on the previous grid points. This ordering and the associated updates are carried out, for instance, during the
first sweep if 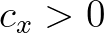 and
and 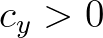 , and the resulting schemes read
, and the resulting schemes read
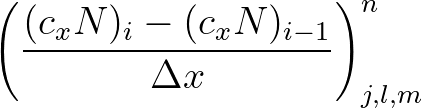 (3.5)
(3.5)
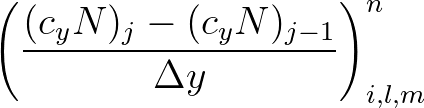 (3.6)
(3.6)
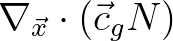 , at the discrete level.
If there is no net flux change in the corresponding grid point, the divergence must be zero, which is obviously the case.
For further details on this solution update, see Section 3.3.
, at the discrete level.
If there is no net flux change in the corresponding grid point, the divergence must be zero, which is obviously the case.
For further details on this solution update, see Section 3.3.
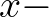 and
and 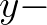 derivatives, respectively, are replaced by
derivatives, respectively, are replaced by
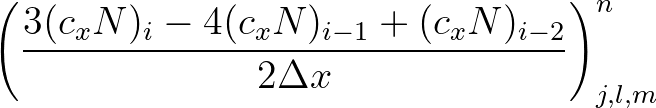 (3.7)
(3.7)
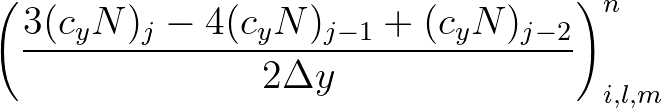 (3.8)
(3.8)
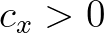 and
and 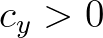 (cf. Section 3.3). See also Rogers et al. (2002).
This scheme, also known as a BDF scheme (Gear, 1971), is second accurate in space,
but first order in time (not relevant), and is flux conservative (empirical evidence), but not monotone.
In addition, this scheme preserves causality and produces less amount of numerical diffusion and is not significantly more expensive than the BSBT scheme.
(cf. Section 3.3). See also Rogers et al. (2002).
This scheme, also known as a BDF scheme (Gear, 1971), is second accurate in space,
but first order in time (not relevant), and is flux conservative (empirical evidence), but not monotone.
In addition, this scheme preserves causality and produces less amount of numerical diffusion and is not significantly more expensive than the BSBT scheme.
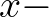 and
and 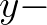 derivatives, respectively, are replaced by
derivatives, respectively, are replaced by
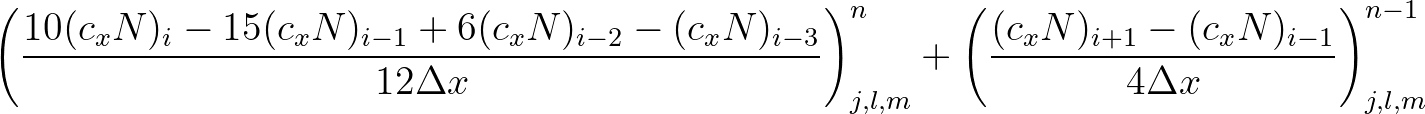 (3.9)
(3.9)
 (3.10)
(3.10)
 and
and 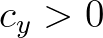 (cf. Section 3.3). See also Rogers et al. (2002).
This scheme is second accurate in time and space, unconditionally stable, preserves causality, and is flux conservative (empirical evidence).
Moreover, the amount of numerical diffusion generated by this scheme is significantly much smaller than both BSBT and SORDUP schemes.
(cf. Section 3.3). See also Rogers et al. (2002).
This scheme is second accurate in time and space, unconditionally stable, preserves causality, and is flux conservative (empirical evidence).
Moreover, the amount of numerical diffusion generated by this scheme is significantly much smaller than both BSBT and SORDUP schemes.
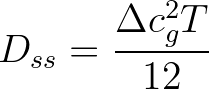 (3.11)
(3.11)
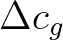 is the difference in the group velocities of successive frequencies, and
is the difference in the group velocities of successive frequencies, and 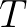 is the so-called wave age, i.e. the time elapsed since the propagated swell was generated by the storm.
The diffusion normal to the propagation direction (locally along the wave crest) is
is the so-called wave age, i.e. the time elapsed since the propagated swell was generated by the storm.
The diffusion normal to the propagation direction (locally along the wave crest) is
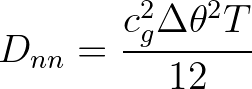 (3.12)
(3.12)
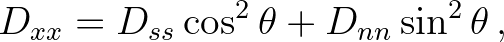 |
|||
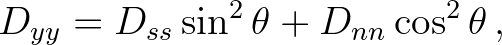 |
|||
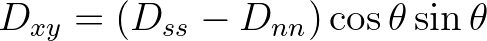 |
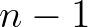 , as follows
, as follows
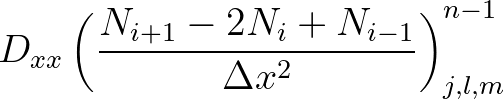 (3.14)
(3.14)
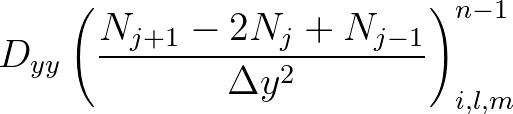 (3.15)
(3.15)
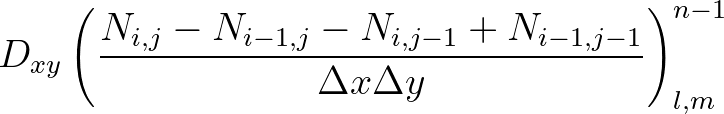 (3.16)
(3.16)
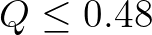 , no instability was observed (Rogers et al., 2002). It is readily shown that for typical ocean applications
, no instability was observed (Rogers et al., 2002). It is readily shown that for typical ocean applications 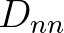 dominates the
diffusion and
dominates the
diffusion and 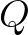 can be written as
can be written as
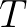 could be computed during the computations of SWAN but it requires the same order of magnitude of computer memory as
integrating the action balance equation. Instead a constant wave age
could be computed during the computations of SWAN but it requires the same order of magnitude of computer memory as
integrating the action balance equation. Instead a constant wave age 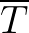 can be used as an approximation, so that Eq. (3.18)
becomes
can be used as an approximation, so that Eq. (3.18)
becomes
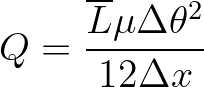 (3.19)
(3.19)
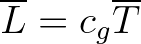 (e.g., the dimension of the ocean basin) and
(e.g., the dimension of the ocean basin) and
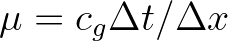 is the Courant number. For
oceanic applications, the Courant number is typically
is the Courant number. For
oceanic applications, the Courant number is typically
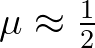 so that
so that
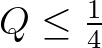 for typical values of
for typical values of
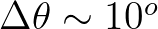 and
and
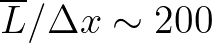 (the number of grid points in one direction of the grid). This implies that the Stelling and Leendertse scheme with the
GSE correction is stable for typical ocean cases. For shelf sea (regional) applications, the value of
(the number of grid points in one direction of the grid). This implies that the Stelling and Leendertse scheme with the
GSE correction is stable for typical ocean cases. For shelf sea (regional) applications, the value of
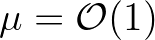 but the garden-sprinkler
effect tends to be small on these scales and the diffusion can and should not be used to avoid the stability problem. For small-scale (local)
applications, typically
but the garden-sprinkler
effect tends to be small on these scales and the diffusion can and should not be used to avoid the stability problem. For small-scale (local)
applications, typically
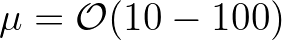 . But such cases are usually treated as stationary and the SORDUP scheme (no GSE
correction is included in this scheme), or preferably the BSBT scheme, should be used. See also Rogers et al. (2002) for further details.
. But such cases are usually treated as stationary and the SORDUP scheme (no GSE
correction is included in this scheme), or preferably the BSBT scheme, should be used. See also Rogers et al. (2002) for further details.
The SWAN team 2024-09-09