Next: Iteration process and stopping Up: Numerical approaches Previous: Conservative elimination of negative
The implicit discretization of the action balance equation (2.19) as described in Section 3.2 yields
a system of linear equations that need to be solved. The corresponding matrix structure can
take different forms, mainly depending on the propagation of wave energy in the geographic space. For instance,
suppose that 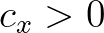 and
and 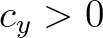 , everywhere. Then, the matrix structure has the following form:
, everywhere. Then, the matrix structure has the following form:
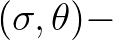 space for each geographic grid point, whereas the off-diagonal subblocks
represent coupling across geographical grid points.
The ordering of grid points is determined by the direction of wave propagation.
This system can be solved with a
Gauss-Seidel technique in one step, if the wave characteristic is a straight line and constant everywhere (Wesseling, 1992).
In addition, this number is independent of grid size. Hence, the complexity of this algorithm is
space for each geographic grid point, whereas the off-diagonal subblocks
represent coupling across geographical grid points.
The ordering of grid points is determined by the direction of wave propagation.
This system can be solved with a
Gauss-Seidel technique in one step, if the wave characteristic is a straight line and constant everywhere (Wesseling, 1992).
In addition, this number is independent of grid size. Hence, the complexity of this algorithm is
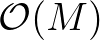 for a total of
for a total of 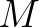 grid points.
grid points.
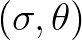 -space, resulting in four quadrants
of each
-space, resulting in four quadrants
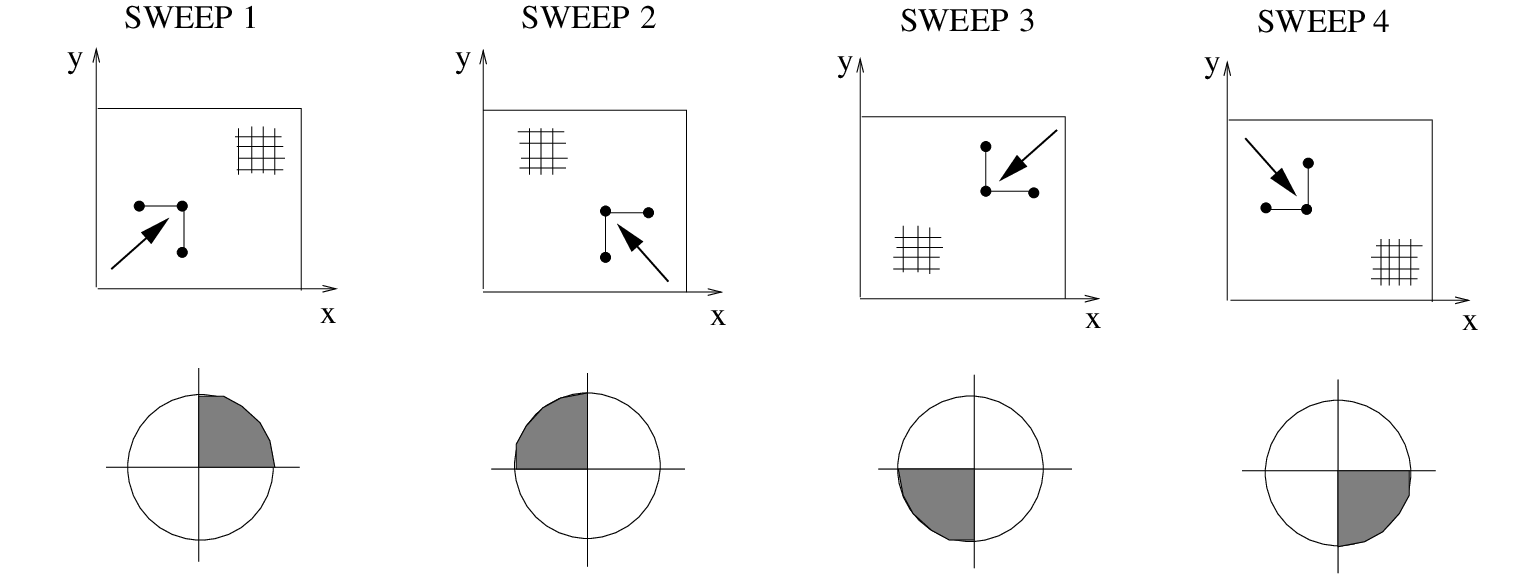
of each 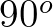 , as illustrated in Figure 3.1. In this case we have four sweeps
and the selected wave directions in each sweep form the domain of dependence appropriate for update. This
immediately satisfies the CFL criterion. This criterion is related to the causality principle.
In general, a numerical scheme must look for information
by following characteristics in an upwind fashion. Causality can be preserved in the
iteration process by means of ordering grid points according to the propagation direction, which guarantees
convergence in a finite number of iterations. We will come back to that later
in Section 3.4.
, as illustrated in Figure 3.1. In this case we have four sweeps
and the selected wave directions in each sweep form the domain of dependence appropriate for update. This
immediately satisfies the CFL criterion. This criterion is related to the causality principle.
In general, a numerical scheme must look for information
by following characteristics in an upwind fashion. Causality can be preserved in the
iteration process by means of ordering grid points according to the propagation direction, which guarantees
convergence in a finite number of iterations. We will come back to that later
in Section 3.4.
 |
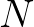 are updated depending on the sign of
are updated depending on the sign of
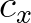 and
and 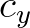 . For instance, the first sweep starts at the lower left hand corner and all grid points
with
. For instance, the first sweep starts at the lower left hand corner and all grid points
with 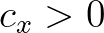 and
and 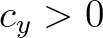 are updated. Because of the causality principle these transport velocities
must be positive in those ordered grid points along the wave ray, in order to make a stable iterative update.
Moreover, adapting the ordering of updates of the unknowns
are updated. Because of the causality principle these transport velocities
must be positive in those ordered grid points along the wave ray, in order to make a stable iterative update.
Moreover, adapting the ordering of updates of the unknowns 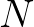 in geographical space to the propagation
direction improves the rate of convergence of the Gauss-Seidel iterative procedure (Wesseling, 1992).
For an illustrative explanation of this technique, see Section 3.5.
in geographical space to the propagation
direction improves the rate of convergence of the Gauss-Seidel iterative procedure (Wesseling, 1992).
For an illustrative explanation of this technique, see Section 3.5.
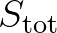 in Eq. (3.2) is nonlinear in
in Eq. (3.2) is nonlinear in 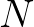 ,
linearization
is required in order to find a solution. Generally, the term
,
linearization
is required in order to find a solution. Generally, the term 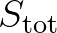 in each bin
in each bin 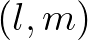 is treated by
distinguishing between positive and negative contributions and arranging these in the linear form
(Ferziger and Perić, 1999):
is treated by
distinguishing between positive and negative contributions and arranging these in the linear form
(Ferziger and Perić, 1999):
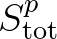 consists of positive contributions and
consists of positive contributions and
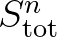 of negative ones. Both contributions are independent of the solution
of negative ones. Both contributions are independent of the solution 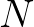 at the corresponding bin
at the corresponding bin 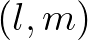 .
Any negative term that does not contain
.
Any negative term that does not contain  as a multiplier is first
divided by
as a multiplier is first
divided by  obtained from the previous iteration level and then added to
obtained from the previous iteration level and then added to 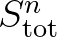 .
This stabilizes the iteration process.
Details on the application of this principle to each source term in SWAN can be found in Booij et al. (1999).
.
This stabilizes the iteration process.
Details on the application of this principle to each source term in SWAN can be found in Booij et al. (1999).
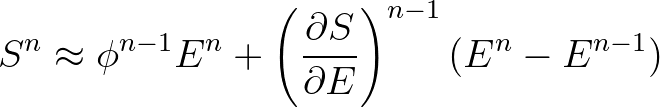 (3.33)
(3.33)
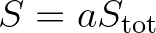 and
and
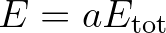 ,
the derivative
,
the derivative
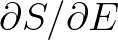 is analytically determined as
is analytically determined as
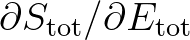 . Here,
. Here,
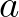 is identical in both expressions and the total energy
is identical in both expressions and the total energy 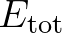 and total source
and total source 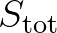 are the integrals
over all frequencies and directions of
are the integrals
over all frequencies and directions of
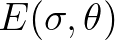 and
and
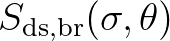 , respectively.
, respectively.
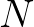 at the corresponding bin and its nearest neighbours:
at the corresponding bin and its nearest neighbours:
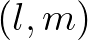 and L(eft), R(ight), B(ottom)
and T(op) correspond to
and L(eft), R(ight), B(ottom)
and T(op) correspond to 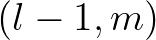 ,
, 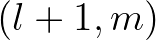 ,
, 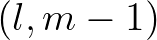 and
and 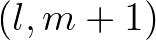 , respectively.
Furthermore, the coefficients
, respectively.
Furthermore, the coefficients
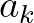 ,
,
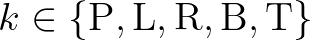 arise from the
discretizations of the fluxes
arise from the
discretizations of the fluxes 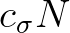 and
and 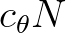 and
and
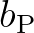 contains the positive contributions
of the source term
contains the positive contributions
of the source term 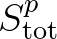 in (3.32) and the updated fluxes
in (3.32) and the updated fluxes 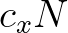 (3.3) and
(3.3) and
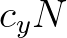 (3.4). Note that coefficient
(3.4). Note that coefficient 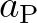 includes
includes
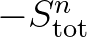 .
.
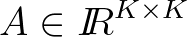 contains the coefficients
contains the coefficients 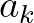 ,
,
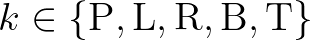 (and
corresponds to a subblock on the main diagonal of (3.31)),
(and
corresponds to a subblock on the main diagonal of (3.31)),
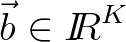 contains the coefficient
contains the coefficient 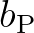 and boundary values and
and boundary values and
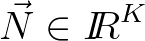 denotes an algebraic vector containing the unknown
action density values. Matrix
denotes an algebraic vector containing the unknown
action density values. Matrix 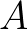 is non-symmetric. The dimension
is non-symmetric. The dimension 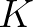 of a
directional quadrant equals
of a
directional quadrant equals
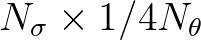 .
Note that linearization of the source term (3.32) enhances diagonal dominance of
.
Note that linearization of the source term (3.32) enhances diagonal dominance of 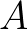 , thereby improving numerical stability.
Also note that neither
, thereby improving numerical stability.
Also note that neither 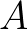 nor
nor 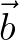 depends on the unknowns.
Each row in the matrix
depends on the unknowns.
Each row in the matrix 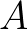 corresponds to a bin
corresponds to a bin
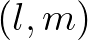 . The main diagonal contains the coefficients
. The main diagonal contains the coefficients
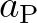 and directly to the left and right are the coefficients
and directly to the left and right are the coefficients
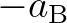 and
and
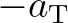 , respectively. The coefficients
, respectively. The coefficients 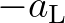 and
and 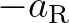 are on the diagonals that are
are on the diagonals that are 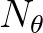 positions to the left and
right of the main diagonal, respectively.
positions to the left and
right of the main diagonal, respectively.
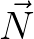 is given by
is given by
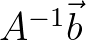 . Since, the only non-zero matrix elements are situated in five diagonals,
iterative solution methods that utilize the sparsity of
. Since, the only non-zero matrix elements are situated in five diagonals,
iterative solution methods that utilize the sparsity of 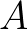 optimally are very attractive.
In SWAN,
the solution of Eq. (3.35) is found by means of an incomplete lower-upper decomposition method followed by an
iteration process called the
Strongly Implicit Procedure (SIP) (Ferziger and Perić, 1999). This procedure is specifically designed for
(non-symmetric) penta-diagonal systems and is relatively fast.
Note that in the absence of mean current there are no shifts
in the frequency, and consequently the structure of
optimally are very attractive.
In SWAN,
the solution of Eq. (3.35) is found by means of an incomplete lower-upper decomposition method followed by an
iteration process called the
Strongly Implicit Procedure (SIP) (Ferziger and Perić, 1999). This procedure is specifically designed for
(non-symmetric) penta-diagonal systems and is relatively fast.
Note that in the absence of mean current there are no shifts
in the frequency, and consequently the structure of 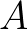 reduces to a tri-diagonal one, i.e.
reduces to a tri-diagonal one, i.e.
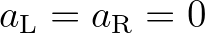 , which can be inverted efficiently with
the Thomas algorithm (Press et al., 1993; Ferziger and Perić, 1999).
, which can be inverted efficiently with
the Thomas algorithm (Press et al., 1993; Ferziger and Perić, 1999).
The SWAN team 2024-09-09