Next: An illustrative explanation of Up: Numerical approaches Previous: Solution algorithm
Generally, the velocities 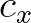 and
and 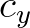 have different
signs in the geographical domain and hence, more steps are needed.
Energy propagates along a wave ray and this cannot be done in 1 iteration as soon as this ray is
curved. Wave rays can be curved in coastal waters due to depth changes and ambient current.
This enhances the number of iterations as it must cover the propagation of energy density along
the whole characteristic curve. The
key issue is the maximum number of iterations needed to cover energy propagation across the
model domain.
have different
signs in the geographical domain and hence, more steps are needed.
Energy propagates along a wave ray and this cannot be done in 1 iteration as soon as this ray is
curved. Wave rays can be curved in coastal waters due to depth changes and ambient current.
This enhances the number of iterations as it must cover the propagation of energy density along
the whole characteristic curve. The
key issue is the maximum number of iterations needed to cover energy propagation across the
model domain.
Any wave ray can be divided into a finite number of pieces so that each piece can be covered
effectively by one of the four sweeps.
This number is related to the directional change of the wave ray.
Since these pieces have to be captured sequentially the total number
of iterations needed is proportional to the number of pieces.
In turn, this number depends on the size of the model domain and the way the
waves propagate through the domain.
If the source terms are included then in every wet grid point a balance between refraction, wind
input, white capping, wave breaking, etc. within the spectral space is evaluated. On top of this
various wave components are marching in the model domain from the open boundaries. It depends
on the strength of the source terms on the one hand and propagation throughout the domain and
the domain size on the other hand how many iterations are actually needed. As a matter of fact,
the total number of iterations depends rather on the local change in wave propagation e.g. in
shallow waters, tidal inlets, and around shoals, irrespective of the ordering and sweeping.
Due to refraction and nonlinear wave energy transfer, interactions occur
between the directional quadrants. To properly take these interactions into
account and the fact that we employ the Gauss-Seidel technique and linearization of the source term (3.32),
the quadrant sweeping and the solution of system (3.35)
need to be repeated until some convergence criteria are met.
The iteration process runs from 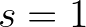 to
to 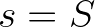 and is terminated if the maximum number of
iterations
and is terminated if the maximum number of
iterations 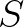 (usually 50) is reached or the following criteria for the significant wave height
(usually 50) is reached or the following criteria for the significant wave height 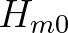 and mean
relative wave period
and mean
relative wave period 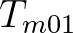 , as given by
, as given by
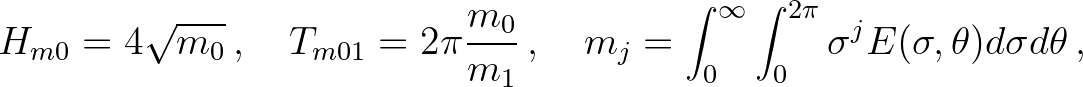 (3.36)
(3.36)
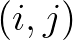 :
:
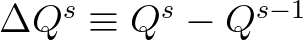 , with
, with 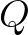 some quantity.
The default values of this limiting criteria are:
some quantity.
The default values of this limiting criteria are:
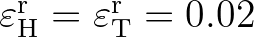 ,
,
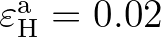 m and
m and
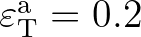 s.
The rationale behind the use of the integral wave parameters
s.
The rationale behind the use of the integral wave parameters
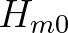 and
and 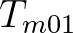 in the stopping criteria is that these are the output variables typically of interest.
The iterative solution procedure is accelerated by calculating a
reasonable first guess of the wave field based on second-generation source
terms of Holthuijsen and De Boer (1988).
in the stopping criteria is that these are the output variables typically of interest.
The iterative solution procedure is accelerated by calculating a
reasonable first guess of the wave field based on second-generation source
terms of Holthuijsen and De Boer (1988).
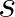 the difference between the successive iterates,
the difference between the successive iterates,
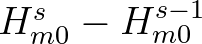 ,
can be small enough to meet the convergence criteria, causing the iteration process to stop, even though
the converged solution has not yet been found. In particular, this happens when convergence is non-monotonic
such that the process is terminated at local maxima or minima that may not coincide with the
converged solution.
,
can be small enough to meet the convergence criteria, causing the iteration process to stop, even though
the converged solution has not yet been found. In particular, this happens when convergence is non-monotonic
such that the process is terminated at local maxima or minima that may not coincide with the
converged solution.
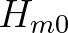 , the quantity
, the quantity 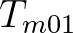 is not an effective measure of
convergence. It was found that the relative error in
is not an effective measure of
convergence. It was found that the relative error in 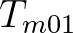 , i.e.
, i.e.
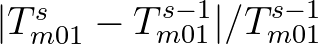 , does not monotonically
decrease near convergence, but keeps
oscillating during the iteration process. This behaviour is due to small variations
in the spectrum at high frequencies, to which
, does not monotonically
decrease near convergence, but keeps
oscillating during the iteration process. This behaviour is due to small variations
in the spectrum at high frequencies, to which 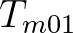 is sensitive.
This
behaviour is problematic when any form of stricter stopping criterion is developed
based on
is sensitive.
This
behaviour is problematic when any form of stricter stopping criterion is developed
based on 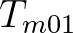 . Therefore, in the improved termination criterion
proposed,
. Therefore, in the improved termination criterion
proposed, 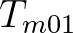 has been abandoned as a convergence
measure and only
has been abandoned as a convergence
measure and only 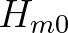 , which displays more monotonic behaviour near
convergence, is retained.
, which displays more monotonic behaviour near
convergence, is retained.
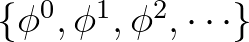 . They show that the actual solution error
is given by
. They show that the actual solution error
is given by
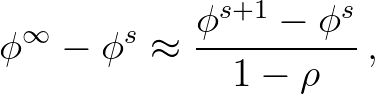 (3.39)
(3.39)
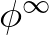 denotes the steady-state solution and
denotes the steady-state solution and 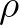 is the spectral radius
indicating the rate of convergence. The smaller
is the spectral radius
indicating the rate of convergence. The smaller 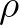 , the faster convergence. This result
shows that the solution error is larger than the difference between successive iterates.
Furthermore, the closer
, the faster convergence. This result
shows that the solution error is larger than the difference between successive iterates.
Furthermore, the closer 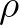 is to 1, the larger the ratio of solution error to the difference
between successive iterates. In other words, the lower the rate of convergence of the
iteration process, the smaller this difference
from one iteration to the next must be to guarantee convergence.
The stopping criterion of SWAN could be improved by making the maximum allowable relative increment
in
is to 1, the larger the ratio of solution error to the difference
between successive iterates. In other words, the lower the rate of convergence of the
iteration process, the smaller this difference
from one iteration to the next must be to guarantee convergence.
The stopping criterion of SWAN could be improved by making the maximum allowable relative increment
in 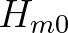 a function of its spectral
radius instead of imposing a fixed allowable
increment. By decreasing the allowable relative increment as
convergence is neared, it would be possible to delay run termination
until a more advanced stage of convergence.
Such a stopping criterion was used by, e.g. Zijlema and Wesseling (1998).
This criterion is adequate
if the iteration process converges in a well-behaved manner and
a function of its spectral
radius instead of imposing a fixed allowable
increment. By decreasing the allowable relative increment as
convergence is neared, it would be possible to delay run termination
until a more advanced stage of convergence.
Such a stopping criterion was used by, e.g. Zijlema and Wesseling (1998).
This criterion is adequate
if the iteration process converges in a well-behaved manner and 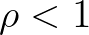 for all iterations.
However, due to nonlinear energy transfer in spectral space SWAN typically does not display such
smooth behaviour. Therefore, this criterion may be less suited for SWAN.
for all iterations.
However, due to nonlinear energy transfer in spectral space SWAN typically does not display such
smooth behaviour. Therefore, this criterion may be less suited for SWAN.
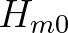 may be expressed in the discrete sense as
may be expressed in the discrete sense as
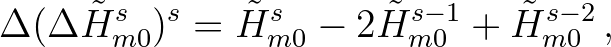 (3.40)
(3.40)
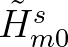 is some measure of the significant wave height at
iteration level
is some measure of the significant wave height at
iteration level 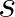 . To eliminate the effect of small amplitude
oscillations on the curvature measure, we define
. To eliminate the effect of small amplitude
oscillations on the curvature measure, we define
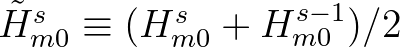 . The resulting curvature-based termination criterion at grid point
. The resulting curvature-based termination criterion at grid point 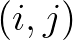 is then
is then
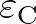 is a given maximum allowable curvature.
The curvature measure is made non-dimensional through normalization with
is a given maximum allowable curvature.
The curvature measure is made non-dimensional through normalization with 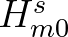 .
Condition
(3.41) must be satisfied in at least 99% of all wet grid points before the iterative process stops.
This curvature requirement is considered to be the primary criterion.
However, the curvature passes through zero between local maxima and minima and, at convergence, the solution
may oscillate between two constant levels due to the action density limiter (see Section 3.7.2), whereas the average curvature is zero.
As safeguard
against such a situation, the weaker criterion (3.37) is retained
in addition to the stricter criterion (3.41).
.
Condition
(3.41) must be satisfied in at least 99% of all wet grid points before the iterative process stops.
This curvature requirement is considered to be the primary criterion.
However, the curvature passes through zero between local maxima and minima and, at convergence, the solution
may oscillate between two constant levels due to the action density limiter (see Section 3.7.2), whereas the average curvature is zero.
As safeguard
against such a situation, the weaker criterion (3.37) is retained
in addition to the stricter criterion (3.41).
The SWAN team 2024-09-09