Next: Solution algorithm Up: Discretization Previous: Discretization in spectral space
The numerical solution obtained with the hybrid central/upwind scheme Eqs. (3.20) and (3.21) is,
in principle, not free from spurious oscillations or wiggles, unless 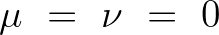 . However, these wiggles will
not result in negative densities in the energy-containing part of the two-dimensional wave
spectrum, as they occur against a background level of energy. On the other hand, the flanks of the spectrum are
immediately adjacent to bins of zero energy. Hence, negative energy prevails especially in these flanks,
either at very low frequencies (
. However, these wiggles will
not result in negative densities in the energy-containing part of the two-dimensional wave
spectrum, as they occur against a background level of energy. On the other hand, the flanks of the spectrum are
immediately adjacent to bins of zero energy. Hence, negative energy prevails especially in these flanks,
either at very low frequencies (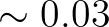 Hz) or in the edges of spread waves, which is likely to be
generated by the hybrid scheme exhibiting numerical dispersion. Since broad banded wave energy field is relatively
smooth away from blocking frequency (low gradients), these negative energy densities tend to be rather small.
They can be effectively removed through the so-called conservative elimination (Tolman, 1991). In short, all
negative energy density for each frequency within a sweep is removed, and the energy densities for
all directions within this directional sector at a given frequency are multiplied by a constant factor
to conserve energy.
Hz) or in the edges of spread waves, which is likely to be
generated by the hybrid scheme exhibiting numerical dispersion. Since broad banded wave energy field is relatively
smooth away from blocking frequency (low gradients), these negative energy densities tend to be rather small.
They can be effectively removed through the so-called conservative elimination (Tolman, 1991). In short, all
negative energy density for each frequency within a sweep is removed, and the energy densities for
all directions within this directional sector at a given frequency are multiplied by a constant factor
to conserve energy.
The conservative elimination algorithm is outlined as follows. For a given frequency 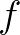 and a given directional
range
and a given directional
range
![$[\theta_1, \theta_2]$](img926.png) of one of the four sweeps, we differentiate between positive and negative contributions
of the energy density, as follows
of one of the four sweeps, we differentiate between positive and negative contributions
of the energy density, as follows
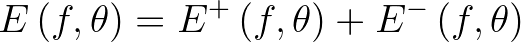 (3.27)
(3.27)
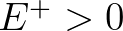 and
and 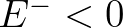 . Next, we compute the total energy within the sweep at frequency
. Next, we compute the total energy within the sweep at frequency 
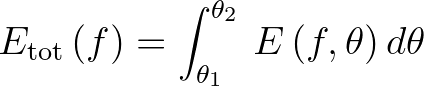 (3.28)
(3.28)
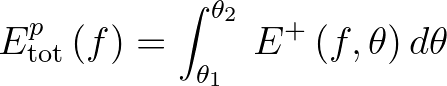 (3.29)
(3.29)
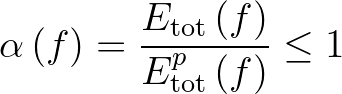 (3.30)
(3.30)
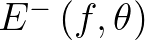 = 0, while the positive
densities are multiplied by factor
= 0, while the positive
densities are multiplied by factor 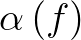 to preserve the total energy at given frequency
to preserve the total energy at given frequency 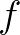 .
.
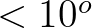 ) distributed over a number of directional bins of
each
) distributed over a number of directional bins of
each 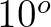 within a sweep. As a result,
within this directional sector the total amount of negative densities can be larger than the amount of
positive ones. This implies
within a sweep. As a result,
within this directional sector the total amount of negative densities can be larger than the amount of
positive ones. This implies 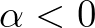 . In such a case, conserving energy within this sweep makes no
sense, and we will then eliminate the negative energy densities and to leave the positive densities as they
are. This is called strict elimination. It must be noted that in that case the hybrid scheme Eq. (3.21)
is inaccurate anyway, and strict elimination will most likely not worsen this case.
. In such a case, conserving energy within this sweep makes no
sense, and we will then eliminate the negative energy densities and to leave the positive densities as they
are. This is called strict elimination. It must be noted that in that case the hybrid scheme Eq. (3.21)
is inaccurate anyway, and strict elimination will most likely not worsen this case.
The SWAN team 2024-09-09