Next: A historical overview of Up: On the approximation of Previous: Energy transport along wave
In this section we discuss how refraction affects the accuracy of the discretization of the total derivative of wave energy along a non-curved wave ray.
Initially, the energy is uniformly distributed over the wave directions.
Under these conditions, we reconsider Eq. (3.47),
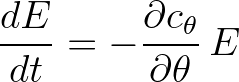 (3.54)
(3.54)
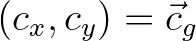 the propagation velocity vector in the geographical space.
This total derivative indicates that the time rate of change in energy is computed along the wave characteristics defined by the following ODEs
the propagation velocity vector in the geographical space.
This total derivative indicates that the time rate of change in energy is computed along the wave characteristics defined by the following ODEs
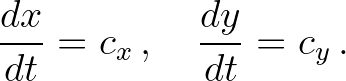 (3.56)
(3.56)
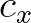 and
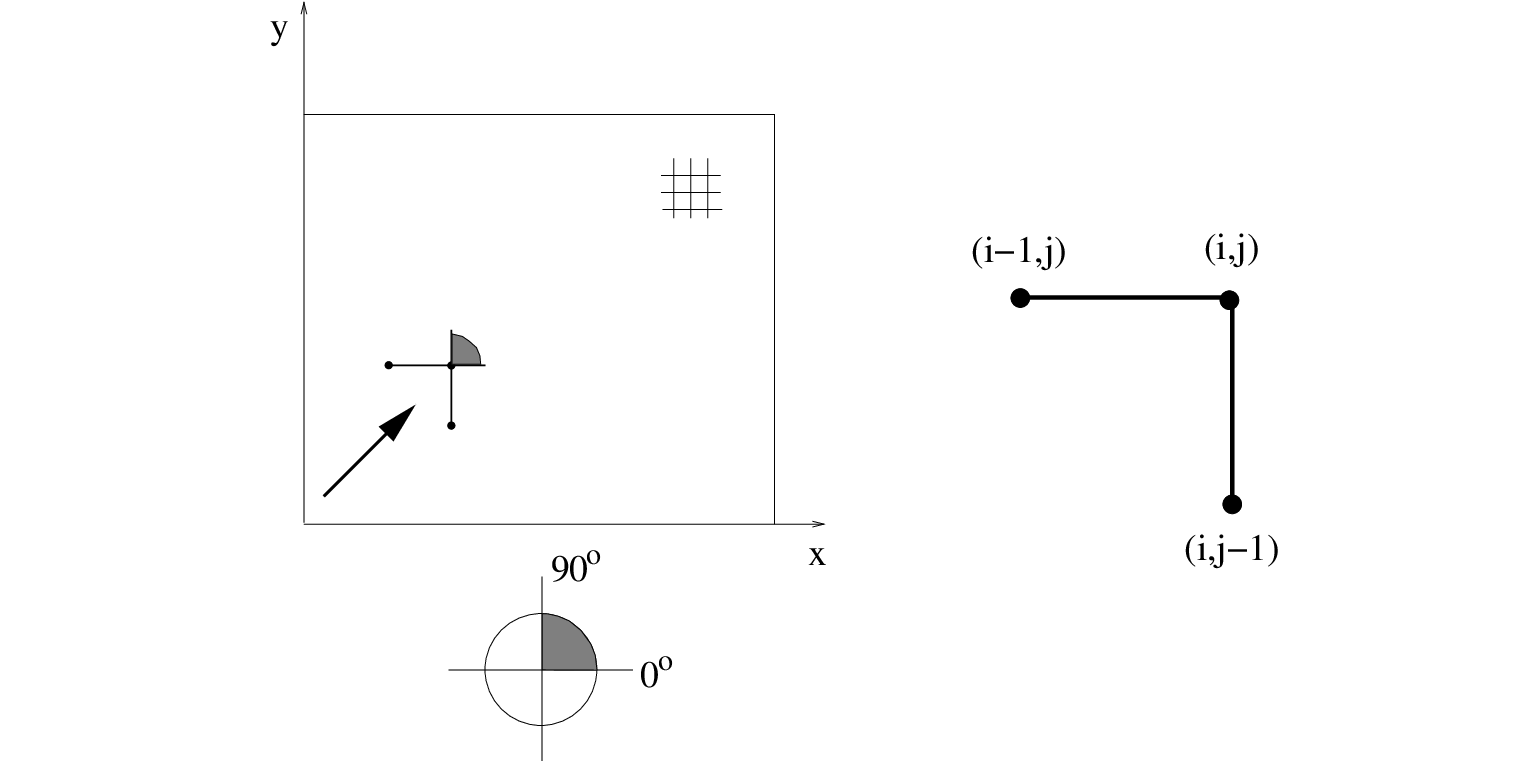
and 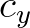 positive during the first sweep, see Figure 3.4,
positive during the first sweep, see Figure 3.4,
 |
 (3.57)
(3.57)
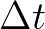 is the time step, and
is the time step, and 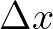 and
and 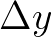 are the mesh spaces. This approximation can be viewed as the well-known semi-Lagrangian approximation, which is rewritten as
are the mesh spaces. This approximation can be viewed as the well-known semi-Lagrangian approximation, which is rewritten as
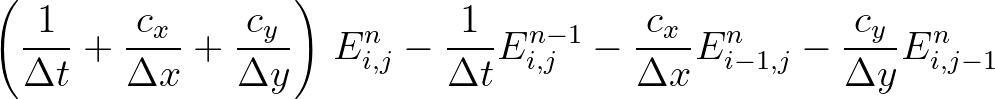 (3.58)
(3.58)
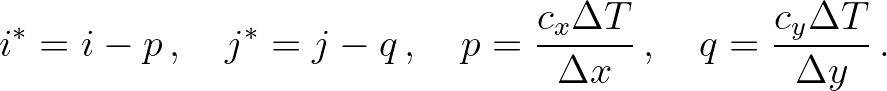 (3.60)
(3.60)
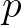 and
and 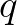 are the Courant numbers. They are not integers, and therefore
are the Courant numbers. They are not integers, and therefore 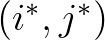 is not a grid point. This point, however, lies on the wave characteristic. The quantity
is not a grid point. This point, however, lies on the wave characteristic. The quantity
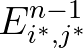 can be
interpreted as the value of
can be
interpreted as the value of 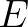 at time
at time 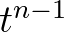 in
in 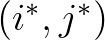 which is being convected in
which is being convected in 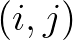 in a lapsed time
in a lapsed time 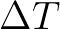 .
This value is simply obtained from the interpolation of the surrounding values
.
This value is simply obtained from the interpolation of the surrounding values 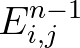 ,
,
 ,
, 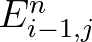 and
and 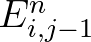 in the
in the 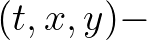 plane. In this case, there is no restriction on time step
plane. In this case, there is no restriction on time step 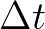 as the characteristic lies inside the computational stencil.
Note that the lapsed time
as the characteristic lies inside the computational stencil.
Note that the lapsed time 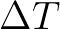 is a function of time step
is a function of time step 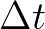 and grid sizes
and grid sizes
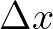 and
and 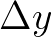 , and is called the Lagrangian time step, which should not be confused with the Eulerian time step
, and is called the Lagrangian time step, which should not be confused with the Eulerian time step 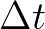 . Generally,
. Generally,
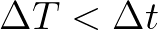 .
.
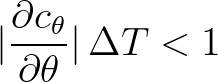 (3.61)
(3.61)
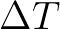 .
Thus, for physical consistency, a restriction on the time step must be imposed in order for the wave directions not to cross each other and the boundaries of a quadrant in the spectral space.
Specifically, the Courant number based on
.
Thus, for physical consistency, a restriction on the time step must be imposed in order for the wave directions not to cross each other and the boundaries of a quadrant in the spectral space.
Specifically, the Courant number based on 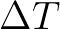 and
and 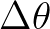 (i.e. directional bin) must be less than unity, that is,
(i.e. directional bin) must be less than unity, that is,
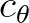 the turning rate3.7.
This condition is a sufficient one and implies the Lipschitz criterion.
the turning rate3.7.
This condition is a sufficient one and implies the Lipschitz criterion.
 ,
see Figure 3.4).
For example, consider the first sweep, see Figure 3.4, the boundaries of the first quadrant are the lines 0
,
see Figure 3.4).
For example, consider the first sweep, see Figure 3.4, the boundaries of the first quadrant are the lines 0 and 90
and 90 . Next, we consider the directional
sector in the spectral space associated with the considered sweep, see Figure 3.5.
We shall show that condition, Eq. (3.62), is sufficient to assure that 1) during
. Next, we consider the directional
sector in the spectral space associated with the considered sweep, see Figure 3.5.
We shall show that condition, Eq. (3.62), is sufficient to assure that 1) during 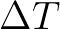 the distance travelled in
the distance travelled in 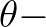 direction is at most
direction is at most
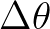 and 2) wave energy propagating in any bin in
and 2) wave energy propagating in any bin in 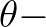 direction will not cross the boundaries of the directional sector,
except for the first and last bins. Hence, this prevents wave rays from intersecting each other.
Note that we implicitly assume that the net change in mean wave direction within the distance covered during
direction will not cross the boundaries of the directional sector,
except for the first and last bins. Hence, this prevents wave rays from intersecting each other.
Note that we implicitly assume that the net change in mean wave direction within the distance covered during 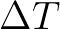 is less than the directional resolution.
Since, by definition,
is less than the directional resolution.
Since, by definition,
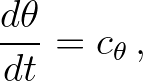 (3.63)
(3.63)
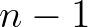 , we choose an arbitrary point,
, we choose an arbitrary point, 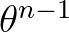 , inside the directional sector; see Figure 3.5.
If
, inside the directional sector; see Figure 3.5.
If
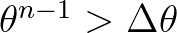 then, Eqs. (3.64) and (3.62) imply
then, Eqs. (3.64) and (3.62) imply
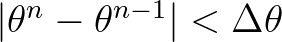 , and hence the chosen point at next time step,
, and hence the chosen point at next time step, 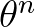 , still lies inside the directional sector. If
, still lies inside the directional sector. If
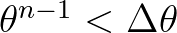 , i.e. in the first bin, then one obtains
, i.e. in the first bin, then one obtains
![$\displaystyle \theta^n = \theta^{n-1} + \frac{\Delta T}{\Delta \theta} \left[ (...
...1}) c_\theta(\theta=0^o) + \theta^{n-1} c_\theta(\theta=\Delta \theta) \right]
$](img1085.png) (3.65)
(3.65)
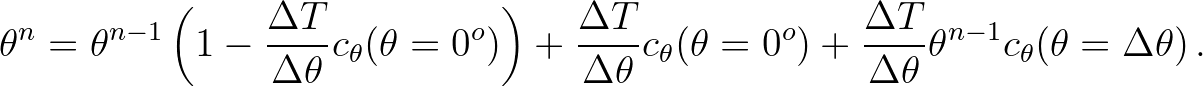 (3.66)
(3.66)
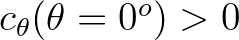 and
and
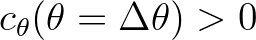 then, the point at next step will be keep inside the directional sector, if Eq. (3.62) holds. In other cases the energy is leaving
through boundary
then, the point at next step will be keep inside the directional sector, if Eq. (3.62) holds. In other cases the energy is leaving
through boundary  , though the change in direction is limited to the adjacent directional bin of the other quadrant.
This holds also for the last bin and the corresponding right boundary
, though the change in direction is limited to the adjacent directional bin of the other quadrant.
This holds also for the last bin and the corresponding right boundary 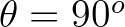 .
.
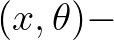 space, propagating at an angle with the positive
space, propagating at an angle with the positive 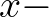 axis.
There is a bottom gradient along this axis so that refraction is present. There are no currents.
The associated characteristic or wave ray is given by
axis.
There is a bottom gradient along this axis so that refraction is present. There are no currents.
The associated characteristic or wave ray is given by
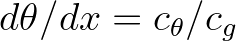 . This is the
spatial turning rate, i.e. the change in wave direction per unit forward distance.
Hence, the directional turn of the wave crest over a distance
. This is the
spatial turning rate, i.e. the change in wave direction per unit forward distance.
Hence, the directional turn of the wave crest over a distance 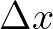 is given by
is given by
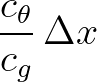 (3.67)
(3.67)
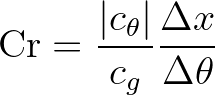 (3.68)
(3.68)
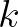 is the wave number,
is the wave number, 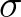 is the frequency,
is the frequency, 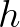 is the water depth and
is the water depth and 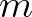 is the coordinate along the wave crest (i.e. orthogonal to the propagation direction). On a coarse grid,
the depth difference in two adjacent grid points
is the coordinate along the wave crest (i.e. orthogonal to the propagation direction). On a coarse grid,
the depth difference in two adjacent grid points 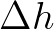 , and thereby
, and thereby 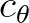 , can be very large, especially for low-frequency components in very shallow water
(see also Section 3.8.5).
This implies that the Lipschitz condition may be violated, i.e.
, can be very large, especially for low-frequency components in very shallow water
(see also Section 3.8.5).
This implies that the Lipschitz condition may be violated, i.e.
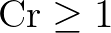 .
.
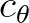 in the shallowest grid point can be simply too large due to a large difference in bottom levels over one mesh width,
so that wave energy will change direction over more than some directional bins
or even the directional sector, so that wave rays falsely intersect each other.
To prevent this artefact a limitation on
in the shallowest grid point can be simply too large due to a large difference in bottom levels over one mesh width,
so that wave energy will change direction over more than some directional bins
or even the directional sector, so that wave rays falsely intersect each other.
To prevent this artefact a limitation on 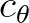 seems to be justified. Recalling Eq. (3.62), a limitation would be
seems to be justified. Recalling Eq. (3.62), a limitation would be
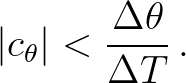 (3.70)
(3.70)
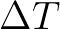 as a fraction of
as a fraction of
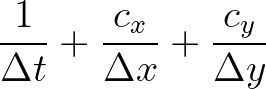 (3.71)
(3.71)
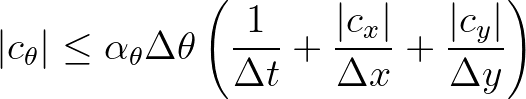 (3.72)
(3.72)
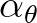 a user-defined maximum Courant number, which is generally smaller than 1. (In SWAN, the default value is
a user-defined maximum Courant number, which is generally smaller than 1. (In SWAN, the default value is
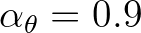 .)
Often the desired time step
.)
Often the desired time step 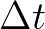 is such that the first term between brackets can be safely neglected. This implies a slightly more restriction
on the turning rate and, in turn, a safety margin in the CFL condition, as follows
is such that the first term between brackets can be safely neglected. This implies a slightly more restriction
on the turning rate and, in turn, a safety margin in the CFL condition, as follows
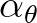 .
In fact, we need to find a good estimate for
.
In fact, we need to find a good estimate for 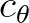 which solely depends on
which solely depends on 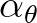 .
However, it is unlikely that this measure affects the solution nearshore or on fine grids, since the turning rate will not too much vary over one (spatial) step.
This is an effective survival measure in the sense that it prevents the excessive refraction without deteriorating the solution
elsewhere.
.
However, it is unlikely that this measure affects the solution nearshore or on fine grids, since the turning rate will not too much vary over one (spatial) step.
This is an effective survival measure in the sense that it prevents the excessive refraction without deteriorating the solution
elsewhere.
The SWAN team 2024-09-09