Next: Implementation of QC approximation Up: On the approximation of Previous: A historical overview of
Another issue is the accuracy with which the turning rate is computed on coarse grids. In SWAN this turning rate is computed as
follows (see also Eq. (3.69))
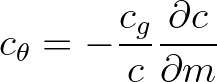 (3.81)
(3.81)
 often inaccurate
often inaccurate  result.
Therefore, Eq. (3.80) is replaced by Eq. (3.82) since version 41.01AB.
result.
Therefore, Eq. (3.80) is replaced by Eq. (3.82) since version 41.01AB.
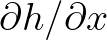 or
or
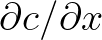 has been approximated using a first order backward difference scheme, for both
structured and unstructured grids,
has been approximated using a first order backward difference scheme, for both
structured and unstructured grids,
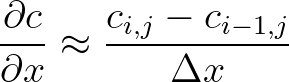 (3.83)
(3.83)
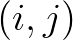 is the shallowest one. This approximation appeared to be rather inaccurate
at coarse grids as well. Moreover, it can also lead to
non-physical asymmetry in turning rate, and therefore wave energy. Therefore, since version 41.01AB, second order central differences are applied as follows
is the shallowest one. This approximation appeared to be rather inaccurate
at coarse grids as well. Moreover, it can also lead to
non-physical asymmetry in turning rate, and therefore wave energy. Therefore, since version 41.01AB, second order central differences are applied as follows
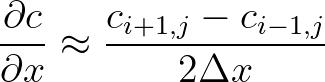 (3.84)
(3.84)
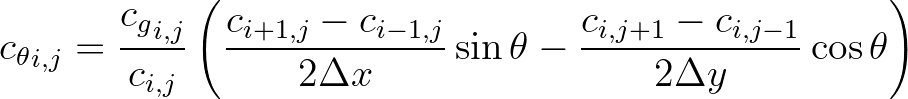 (3.85)
(3.85)
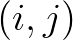 is the shallowest one and that the division by
is the shallowest one and that the division by 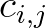 is not correct, i.e. it is not consistent with the Snel's law! It will overestimate
the rate of turning. This error becomes rather large when bottom slopes are exceptionally large
so that wave energy may turn over more than one directional bin. This justifies again the use of the refraction limiter, Eq. (3.73). An appropriate upper bound
is obtained with
is not correct, i.e. it is not consistent with the Snel's law! It will overestimate
the rate of turning. This error becomes rather large when bottom slopes are exceptionally large
so that wave energy may turn over more than one directional bin. This justifies again the use of the refraction limiter, Eq. (3.73). An appropriate upper bound
is obtained with
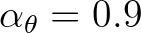 that particularly holds for relative long waves3.8. For shorter waves, a smaller upper bound may be chosen (e.g.
that particularly holds for relative long waves3.8. For shorter waves, a smaller upper bound may be chosen (e.g.
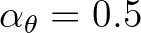 ). However, one may choose a larger CFL upper
bound. For instance, referring to Figure 3.6, i.e. parallel depth contours within 90
). However, one may choose a larger CFL upper
bound. For instance, referring to Figure 3.6, i.e. parallel depth contours within 90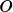 , waves can not turn more than 90
, waves can not turn more than 90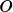 (in line with the Snel's law),
which implies
(in line with the Snel's law),
which implies
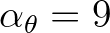 , if
, if
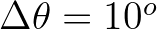 .
.
The SWAN team 2024-09-09