Next: The problem with refraction Up: On the approximation of Previous: The problem with refraction
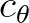
The problem with refraction showing some inaccurate results has been known for a long time. This issue had received some attention by Nico Booij for the first time in November 1998. His basic idea to fix this problem is as follows. We consider a case with parallel depth contours within one sector, see Figure 3.6.
We assume that grid point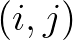 is in shallow water. The other two grid points
is in shallow water. The other two grid points 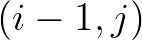 and
and 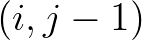 are in deeper water.
Let
are in deeper water.
Let 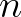 be the coordinate along the wave rays.
Then according to Snel's law (Holthuijsen, 2007, NOTE 7A, pg. 207), we have
be the coordinate along the wave rays.
Then according to Snel's law (Holthuijsen, 2007, NOTE 7A, pg. 207), we have
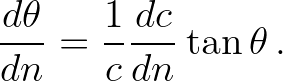 (3.74)
(3.74)
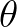 will be of the order of 45
will be of the order of 45 . So, we get
. So, we get
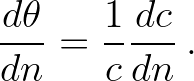 (3.75)
(3.75)
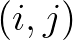 determines the value of
determines the value of  . In shallow water,
. In shallow water, 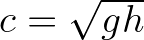 , so
, so
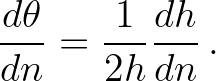 (3.76)
(3.76)
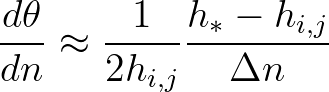 (3.77)
(3.77)
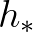 the water depth in one of the neighbouring grid points
the water depth in one of the neighbouring grid points 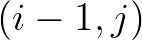 and
and 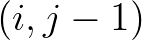 . In the numerical procedure
. In the numerical procedure 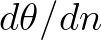 is constant over a spatial step, so the change in direction over a step is
is constant over a spatial step, so the change in direction over a step is
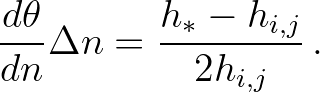 (3.78)
(3.78)
 . Consequently, we obtain
. Consequently, we obtain
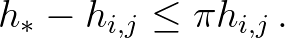 (3.79)
(3.79)
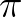 is replaced by a user-determined factor
is replaced by a user-determined factor 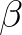 . Hence, the depths in surrounding grid points are reduced to
. Hence, the depths in surrounding grid points are reduced to 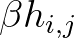 , if they are larger than this value.
It should be noted that this approach was outlined in an unpublished note. Our experience with this approach is that it seems not effective enough.
, if they are larger than this value.
It should be noted that this approach was outlined in an unpublished note. Our experience with this approach is that it seems not effective enough.
The SWAN team 2024-09-09