Next: Calculation of diffusion-like terms Up: Unstructured mesh implementation Previous: Interpolation at user-defined locations
FORCE is the wave-driven stress, i.e. the force per unit surface driving the wave-driven current, expressed in N/m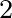 , is defined
as the gradient of the radiation stresses:
, is defined
as the gradient of the radiation stresses:
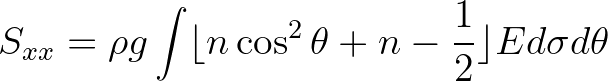 (8.30)
(8.30)
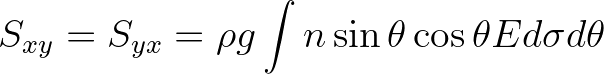 (8.31)
(8.31)
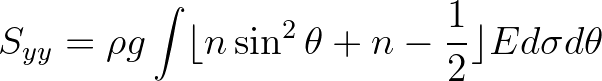 (8.32)
(8.32)
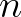 the ratio of group velocity and phase velocity.
The force is then
the ratio of group velocity and phase velocity.
The force is then
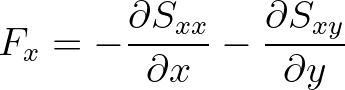 (8.33)
(8.33)
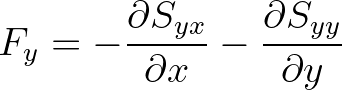 (8.34)
(8.34)
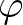 be one of the
radiation stresses
be one of the
radiation stresses 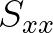 ,
, 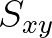 and
and 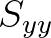 . The gradient of
. The gradient of  is computed as follows
is computed as follows
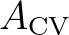 is the area of the CV and the summation runs over the associated edges
is the area of the CV and the summation runs over the associated edges  of this CV.
The values
of this CV.
The values 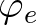 at edges of the centroid dual are taken as averages, i.e.
at edges of the centroid dual are taken as averages, i.e.
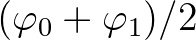 ,
,
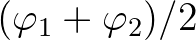 , etc.
Moreover, the value of the radiation stresses
inside each triangle is simply the average of the radiation stresses in the associated vertices of the cell. Now, the derivatives of
, etc.
Moreover, the value of the radiation stresses
inside each triangle is simply the average of the radiation stresses in the associated vertices of the cell. Now, the derivatives of 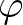 inside
CV are
inside
CV are
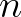 the number of surrounding cells of the considered vertex and
the number of surrounding cells of the considered vertex and
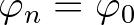 ,
, 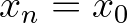 and
and 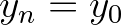 .
The area of the CV is given by
.
The area of the CV is given by
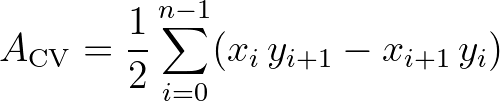 (8.38)
(8.38)
The SWAN team 2024-09-09