Next: Computation of wave-induced force Up: Unstructured mesh implementation Previous: The sweeping algorithm
All the quantities deals with in SWAN are located at the vertices. Hence, due to the user-defined locations of the wave parameters, interpolations are required.
Let parameter
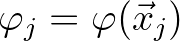 and Cartesian coordinates
and Cartesian coordinates
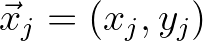 , with
, with
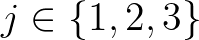 indicating the vertices of cell
indicating the vertices of cell 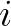 , be given.
The vertices 1, 2 and 3 are ordered in a counterclockwise direction, see Figure 8.2. The associated 3 edges are denoted as 12, 23 and 31.
, be given.
The vertices 1, 2 and 3 are ordered in a counterclockwise direction, see Figure 8.2. The associated 3 edges are denoted as 12, 23 and 31.
Linear interpolation, with 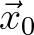 inside cell
inside cell 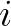 and
and
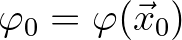 , is given by
, is given by
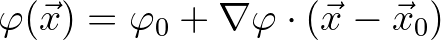 (8.17)
(8.17)
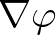 is a constant vector inside cell
is a constant vector inside cell 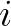 . We apply Green-Gauss reconstruction, i.e.,
. We apply Green-Gauss reconstruction, i.e.,
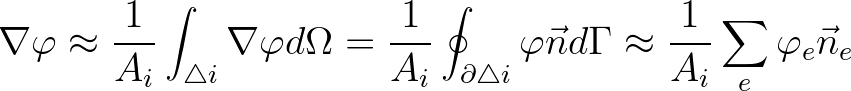 (8.18)
(8.18)
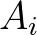 is the area of cell
is the area of cell 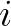 and the summation runs over the 3 edges
and the summation runs over the 3 edges
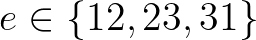 of cell
of cell 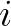 .
The values
.
The values 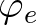 at edges are taken as averages:
at edges are taken as averages:
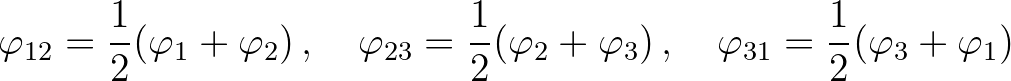 (8.19)
(8.19)
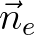 is the outward pointing normal
at edge
is the outward pointing normal
at edge  and is obtained by rotating the edge over 90
and is obtained by rotating the edge over 90 in the clockwise
direction. Hence,
in the clockwise
direction. Hence,
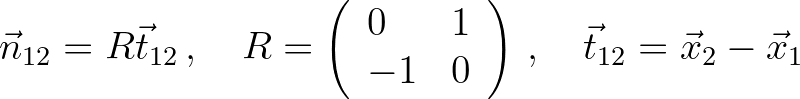 (8.20)
(8.20)
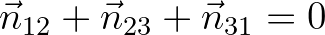 (8.21)
(8.21)
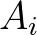 of cell
of cell 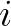 is given by
is given by
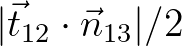 . Hence, with
. Hence, with
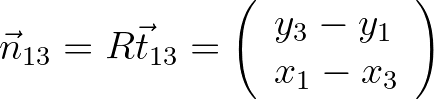 (8.25)
(8.25)
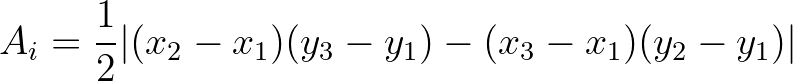 (8.26)
(8.26)
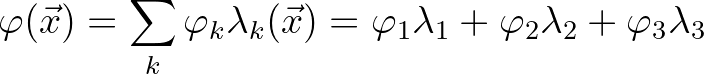 (8.27)
(8.27)
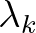 is a linear shape function with the following properties:
is a linear shape function with the following properties:
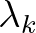 is linear per cell and
is linear per cell and
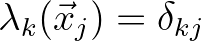 with
with 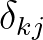 is the Kronecker delta.
is the Kronecker delta.
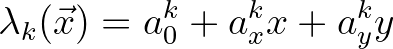 (8.28)
(8.28)
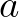 follow from solving
follow from solving
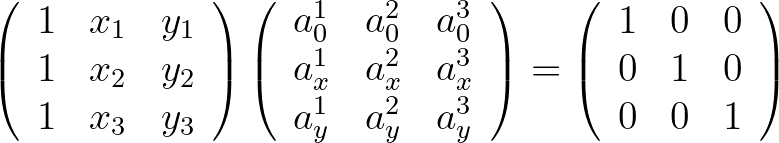 (8.29)
(8.29)
The SWAN team 2024-09-09