Next: Interpolation at user-defined locations Up: Numerical method Previous: Discretization procedure
The solution of each vertex must be updated geographically before proceeding to the next one. For example, referring to Figure 8.2,
the value in vertex 1 is determined by its two upwave vertices 2 and 3 only if they are already updated. In this way causality can be preserved.
For regular grids, the four-sweep scheme based on a four-direction Gauss-Seidel relaxation is employed as outlined in Section 3.3.
The grid points are ordered in a natural manner, e.g. left to right and bottom to top during the first sweep, right to left and bottom to top during the second
sweep, and so on. Hence, the updated values will be used immediately for updating the next unknown.
However, in an unstructured mesh there are no distinct directions. Thus the vertices are ordered by their numbering which for
an unstructured grid are quite random. As a consequence, the latest obtained solution will not necessarily be used for updating surrounding vertices.
Also, we select wave directions in every triangular cell around a vertex for an update in spectral space. This selection differs for each vertex.
An ordering is proposed such that the solution of each vertex will tend to ensure that updated values from the surrounding vertices are used as soon as they are available.
This ordering of vertices is perpendicular to the main wave direction and thus along the wave crests. Usually, the main wave direction is the direction of the incoming wave
energy on the imposed boundary or the wind direction.
All the vertices are ordered according to their distances to the origin of the grid in ascending order.
It is expected that this so-called crest ordering, by which we update along wave characteristics as much as possible, should result in a faster convergence than a
random ordering of vertices. This ordering is usually fine for wind waves or swells propagating along rather straight wave characteristics.
However, it might be less efficient in case of waves propagated along (strong) curved wave rays (e.g. around islands).
In that case the iteration process is not effectively Gauss-Seidel.
Like the structured grid case, a fixed number of sweeps (not necessarily 4) is introduced.
Each sweep represents a range of wave directions that is equal to 2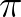 divided by the number of sweeps. As an illustrative example we choose 3 sweeps of each 120
divided by the number of sweeps. As an illustrative example we choose 3 sweeps of each 120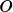 .
For each sweep the vertices are ordered in line with the corresponding sweep direction. The first sweep direction is the dominant wave direction, the second one equals the first one
plus 120
.
For each sweep the vertices are ordered in line with the corresponding sweep direction. The first sweep direction is the dominant wave direction, the second one equals the first one
plus 120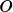 and the last one equals the first one minus 120
and the last one equals the first one minus 120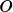 . Hence, we have three different ordering of vertices.
This will speed up the iteration process because propagation of wave energy in other directions is covered as well.
In general, the higher the number of sweeps, the smaller the directional interval, the better the wave energy in various directions is captured in one series of sweeps, the lesser the
number of required iterations to obtain the steady-state convergence (see also Section 3.5). However, by enhancing the number of sweeps, the amount
of computations will be increased as well and thus more computing intensive. Experiences have shown that three sweeps is a good compromise between the reduced number of iterations and
the extended amount of required computation time.
. Hence, we have three different ordering of vertices.
This will speed up the iteration process because propagation of wave energy in other directions is covered as well.
In general, the higher the number of sweeps, the smaller the directional interval, the better the wave energy in various directions is captured in one series of sweeps, the lesser the
number of required iterations to obtain the steady-state convergence (see also Section 3.5). However, by enhancing the number of sweeps, the amount
of computations will be increased as well and thus more computing intensive. Experiences have shown that three sweeps is a good compromise between the reduced number of iterations and
the extended amount of required computation time.
An algorithm is employed that consists of simply proceeding through a list of vertices per sweep that remain to be updated. This list is sorted according to the ascending distances
of vertices to the origin of the grid in line with the sweep direction.
This algorithm goes along with an iteration process. Initially, all vertices are non-updated in both geographic and spectral spaces.
In each iteration, a number of sweeps through the vertices is executed, while the solution of each vertex must be updated geographically before proceeding to the next one.
The two upwave faces connecting the vertex to be updated enclose those wave directions that can be processed in the spectral space; see Figure 8.2.
The solution of each cell having a vertex as one of their vertices and (partly) enclosed by the present sweep must be updated.
The vertex is updated when all cells around this vertex have been considered.
As such, all wave directions can be covered efficiently. The process continues with the next vertex in the list of
non-updated vertices. A sweep is complete when all vertices are updated geographically (but not necessarily in whole spectral space, e.g. due to refraction and
quadruplets). An iteration is complete when all sweeps have been carried out and so all vertices are updated in both geographic and spectral spaces so that wave energy
from all directions has been propagated through geographical space.
This numerical process is iterated until an a priori convergence condition is satisfied. Here, the curvature-based stopping criteria
as outlined in Section 3.4 will be applied. The total number of iterations depends mainly on local change in propagation direction due to bed changes
and ambient current, and possibly also on the domain size. See also Section 3.4 for further details.
The SWAN team 2024-09-09