To establish a criterion with which the truncation of the exponential series function in (2.217) is carried out,
we define the following length scales. Let 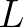 ,
, 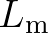 and
and 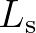 denote the characteristic wave length, the characteristic length scale of medium variation
and the characteristic length scale over which second order wave statistics vary in physical space, respectively.
Since our starting point in the present analysis is Eq. (2.203), thus assuming the medium changing slowly, it is required that the ratio
denote the characteristic wave length, the characteristic length scale of medium variation
and the characteristic length scale over which second order wave statistics vary in physical space, respectively.
Since our starting point in the present analysis is Eq. (2.203), thus assuming the medium changing slowly, it is required that the ratio
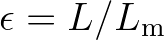 is small.
Hence, the physical validity of Eq. (2.217) remains unaffected by assuming
is small.
Hence, the physical validity of Eq. (2.217) remains unaffected by assuming
 .
In addition, the statistics of the wave field (including cross correlations) is assumed to vary weakly on distances of the order of
.
In addition, the statistics of the wave field (including cross correlations) is assumed to vary weakly on distances of the order of
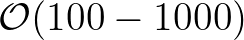 wave
lengths2.10, that is, the ratio
wave
lengths2.10, that is, the ratio
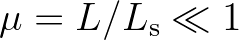 .
.
Next, we introduce the correlation (or coherent) length scale of the wave field 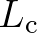 . It measures the correlation between two wave components separated by the distance
. It measures the correlation between two wave components separated by the distance 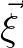 .
Generally, the correlation function
.
Generally, the correlation function
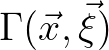 tends to zero as
tends to zero as
 (Smit et al., 2015a).
In particular, for narrow-band waves, the wave field remains correlated over many wave lengths, whereas the coherent radius of directionally spread sea states is relatively small.
So,
(Smit et al., 2015a).
In particular, for narrow-band waves, the wave field remains correlated over many wave lengths, whereas the coherent radius of directionally spread sea states is relatively small.
So, 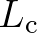 is directly related to the characteristic width of the spectrum
is directly related to the characteristic width of the spectrum 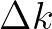 as
as
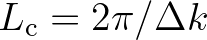 (Smit and Janssen, 2013; Smit et al., 2015a).
We note that the spectrum width
(Smit and Janssen, 2013; Smit et al., 2015a).
We note that the spectrum width 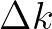 may be measured by the standard deviation of the incident wave field, which is usually statistically quasi-homogeneous.
may be measured by the standard deviation of the incident wave field, which is usually statistically quasi-homogeneous.
Finally, to relate the correlation length scale to the medium variation length scale, we consider the ratio
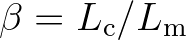 .
This is the key for establishing a suitable approximation to Eq. (2.217). We address two cases of interest, namely,
(i)
.
This is the key for establishing a suitable approximation to Eq. (2.217). We address two cases of interest, namely,
(i)  , in which the wave field de-correlates over distances short compared to the medium variations; and (ii)
, in which the wave field de-correlates over distances short compared to the medium variations; and (ii)
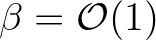 where seabed or current
varies rapidly within the coherent radius of the wave field.
where seabed or current
varies rapidly within the coherent radius of the wave field.
The step in getting explicit approximations is to truncate appropriately the expansion of the exponential function in Eq. (2.217). To this end, consider a wave field
at point 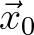 and described by the carrier wave number
and described by the carrier wave number 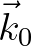 . As parameter
. As parameter 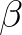 indicates the relative importance of the medium variation (related to
indicates the relative importance of the medium variation (related to
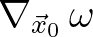 ) with respect to the coherent radius of the wave field (related to
) with respect to the coherent radius of the wave field (related to
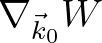 ), the first term in the exponential function is scaled by
), the first term in the exponential function is scaled by
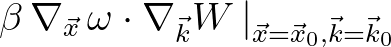 (2.217)
(2.217)
Similarly, parameter 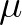 expresses the significance of the spatial variation of the spectrum with respect to the wave length scale (related to
expresses the significance of the spatial variation of the spectrum with respect to the wave length scale (related to
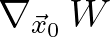 ),
so that the second term of the exponential scaled as
),
so that the second term of the exponential scaled as
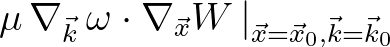 (2.218)
(2.218)
(Note that the group velocity
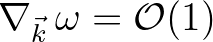 .)
.)
Now, under the conditions that  and also that the
wave field de-correlates on shorter scales than the scale of the medium variations, that is,
and also that the
wave field de-correlates on shorter scales than the scale of the medium variations, that is,  ,
the Taylor series expansion around the phase space point
,
the Taylor series expansion around the phase space point
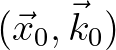 can be expressed as
can be expressed as
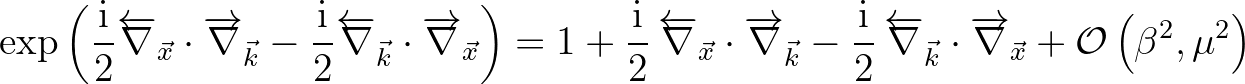 (2.219)
(2.219)
On substitution into Eq (2.217) and neglecting higher order terms we obtain the familiar form for the action balance equation
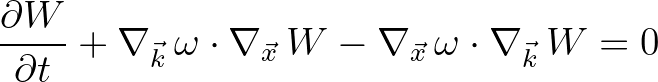 (2.220)
(2.220)
which is thus the lowest order approximation of Eq. (2.217).
At this point, the above analysis is only limited to cases in which  as the truncated expansion in
as the truncated expansion in 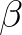 is no longer valid for
is no longer valid for
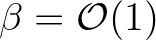 .
A different path is presented here, paved by Smit and Janssen (2013), to extend the range of applicability of the approximate model to values of
.
A different path is presented here, paved by Smit and Janssen (2013), to extend the range of applicability of the approximate model to values of
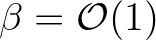 .
.
We recall the Weyl symbol 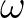 that reads
that reads
with
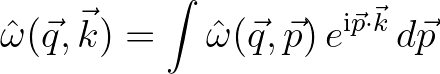 (2.221)
(2.221)
Consequently, the Moyal product yields
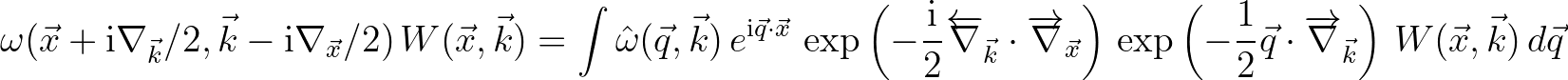 (2.222)
(2.222)
Observing that the assumption  still holds and that the term
still holds and that the term
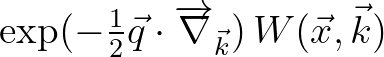 equals
the Taylor series of
equals
the Taylor series of
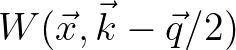 , the phase-space equation is given by
, the phase-space equation is given by
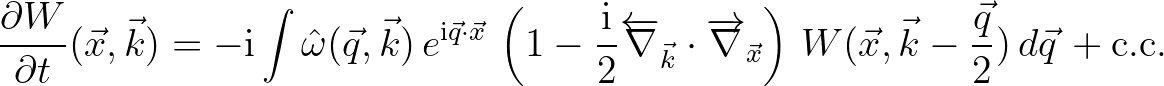 (2.223)
(2.223)
Note that the integral expression is treated as a convolution between 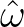 and
and 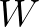 (including their derivatives).
Eq. (2.224) is the central result of the paper of Smit and Janssen (2013) (see their Eq. (15). But see also Akrish et al. (2020), their Eq. (2.19), where the mean currents have been included.)
By virtue of the assumption
(including their derivatives).
Eq. (2.224) is the central result of the paper of Smit and Janssen (2013) (see their Eq. (15). But see also Akrish et al. (2020), their Eq. (2.19), where the mean currents have been included.)
By virtue of the assumption  , they refer to this approximation as the (first order) quasi-coherent (QC) approximation.
, they refer to this approximation as the (first order) quasi-coherent (QC) approximation.
The purpose of the rest of the work presented here is to make the QC approximation numerically more amenable by recasting Eq. (2.224) in the following form
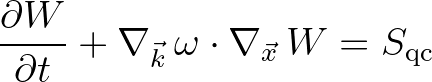 (2.224)
(2.224)
where 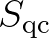 is a scattering source term that accounts for the generation and propagation of inhomogeneous wave field induced by medium variations, including wave
refraction, Doppler shifting2.11 and wave interference.
is a scattering source term that accounts for the generation and propagation of inhomogeneous wave field induced by medium variations, including wave
refraction, Doppler shifting2.11 and wave interference.
We revisit the convolution integral in Eq. (2.224) in order to find a form for 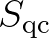 that can be efficiently computed; it is denoted by
that can be efficiently computed; it is denoted by
 .
We consider a point
.
We consider a point
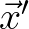 in the neighborhood of the origin.
Then let
in the neighborhood of the origin.
Then let
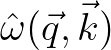 be the Fourier transform of
be the Fourier transform of
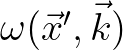 , as follows
, as follows
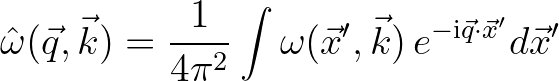 (2.225)
(2.225)
Furthermore, we have (cf. Eq. (2.196))
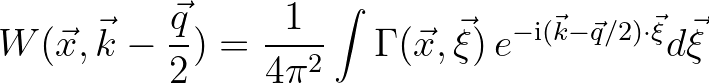 (2.226)
(2.226)
Substituting both of these Fourier transforms in the integral yields
Since the inverse Fourier transform of the (complex) exponential is a shifted Dirac delta, the triple integral is then rewritten as
The last line essentially implies that function
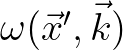 must have a compact support in
must have a compact support in
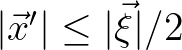 .
Since, by nature, the correlation function is compactly supported,
that is,
.
Since, by nature, the correlation function is compactly supported,
that is,
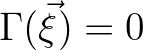 for
for
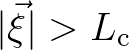 (note
(note
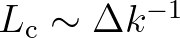 is finite), it is concluded that
the local wave statistics can only be affected by the medium within a radius
is finite), it is concluded that
the local wave statistics can only be affected by the medium within a radius 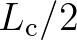 around point
around point  .
.
Following Akrish et al. (2020), the dispersion relation at the point
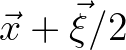 is expressed as a superposition of the local value at
is expressed as a superposition of the local value at  and a remainder,
and a remainder,
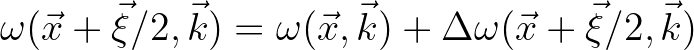 .
Then substitution gives
.
Then substitution gives
We recall Eq. (2.224) and substitute the final expression with the result
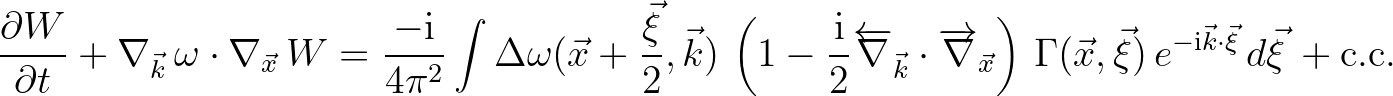 (2.227)
(2.227)
Finally, the source term in its suitable form is obtained by transforming back
with
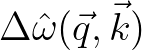 the Fourier transform of
the Fourier transform of
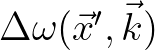 .
By shifting the origin to the point
.
By shifting the origin to the point  , the Fourier transform of
, the Fourier transform of
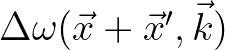 is then given by
is then given by
 (2.228)
(2.228)
This Fourier transform is denoted by
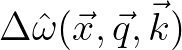 and is computed over a square domain with a fixed size
and is computed over a square domain with a fixed size 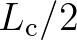 around the point
around the point  .
It should be noted that the source term
.
It should be noted that the source term 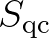 is evaluated by means of integration over
is evaluated by means of integration over 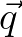 and not over
and not over 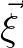 .
.
In summary, the evolution equation for the Wigner distribution is given by Eq. (2.225), whereas
the QC scattering term that describes the evolution of the coherent structures in the wave field reads
The SWAN team 2024-09-09
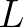 ,
, 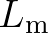 and
and 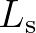 denote the characteristic wave length, the characteristic length scale of medium variation
and the characteristic length scale over which second order wave statistics vary in physical space, respectively.
Since our starting point in the present analysis is Eq. (2.203), thus assuming the medium changing slowly, it is required that the ratio
denote the characteristic wave length, the characteristic length scale of medium variation
and the characteristic length scale over which second order wave statistics vary in physical space, respectively.
Since our starting point in the present analysis is Eq. (2.203), thus assuming the medium changing slowly, it is required that the ratio
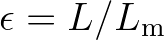 is small.
Hence, the physical validity of Eq. (2.217) remains unaffected by assuming
is small.
Hence, the physical validity of Eq. (2.217) remains unaffected by assuming
 .
In addition, the statistics of the wave field (including cross correlations) is assumed to vary weakly on distances of the order of
.
In addition, the statistics of the wave field (including cross correlations) is assumed to vary weakly on distances of the order of
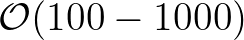 wave
lengths2.10, that is, the ratio
wave
lengths2.10, that is, the ratio
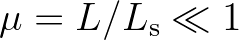 .
.
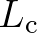 . It measures the correlation between two wave components separated by the distance
. It measures the correlation between two wave components separated by the distance 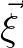 .
Generally, the correlation function
.
Generally, the correlation function
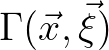 tends to zero as
tends to zero as
 (Smit et al., 2015a).
In particular, for narrow-band waves, the wave field remains correlated over many wave lengths, whereas the coherent radius of directionally spread sea states is relatively small.
So,
(Smit et al., 2015a).
In particular, for narrow-band waves, the wave field remains correlated over many wave lengths, whereas the coherent radius of directionally spread sea states is relatively small.
So, 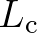 is directly related to the characteristic width of the spectrum
is directly related to the characteristic width of the spectrum 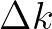 as
as
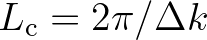 (Smit and Janssen, 2013; Smit et al., 2015a).
We note that the spectrum width
(Smit and Janssen, 2013; Smit et al., 2015a).
We note that the spectrum width 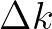 may be measured by the standard deviation of the incident wave field, which is usually statistically quasi-homogeneous.
may be measured by the standard deviation of the incident wave field, which is usually statistically quasi-homogeneous.
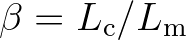 .
This is the key for establishing a suitable approximation to Eq. (2.217). We address two cases of interest, namely,
(i)
.
This is the key for establishing a suitable approximation to Eq. (2.217). We address two cases of interest, namely,
(i)  , in which the wave field de-correlates over distances short compared to the medium variations; and (ii)
, in which the wave field de-correlates over distances short compared to the medium variations; and (ii)
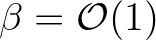 where seabed or current
varies rapidly within the coherent radius of the wave field.
where seabed or current
varies rapidly within the coherent radius of the wave field.
 and described by the carrier wave number
and described by the carrier wave number 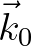 . As parameter
. As parameter 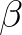 indicates the relative importance of the medium variation (related to
indicates the relative importance of the medium variation (related to
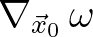 ) with respect to the coherent radius of the wave field (related to
) with respect to the coherent radius of the wave field (related to
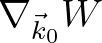 ), the first term in the exponential function is scaled by
), the first term in the exponential function is scaled by
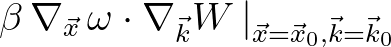 (2.217)
(2.217)
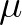 expresses the significance of the spatial variation of the spectrum with respect to the wave length scale (related to
expresses the significance of the spatial variation of the spectrum with respect to the wave length scale (related to
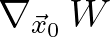 ),
so that the second term of the exponential scaled as
),
so that the second term of the exponential scaled as
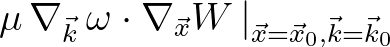 (2.218)
(2.218)
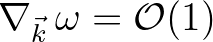 .)
.)
 and also that the
wave field de-correlates on shorter scales than the scale of the medium variations, that is,
and also that the
wave field de-correlates on shorter scales than the scale of the medium variations, that is,  ,
the Taylor series expansion around the phase space point
,
the Taylor series expansion around the phase space point
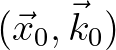 can be expressed as
can be expressed as
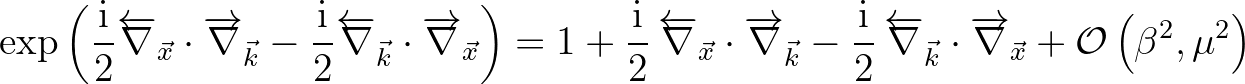 (2.219)
(2.219)
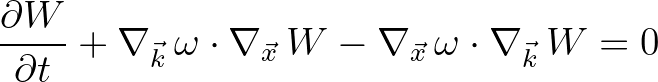 (2.220)
(2.220)
 as the truncated expansion in
as the truncated expansion in 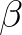 is no longer valid for
is no longer valid for
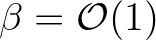 .
A different path is presented here, paved by Smit and Janssen (2013), to extend the range of applicability of the approximate model to values of
.
A different path is presented here, paved by Smit and Janssen (2013), to extend the range of applicability of the approximate model to values of
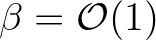 .
.
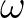 that reads
that reads
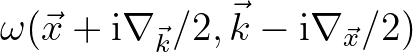

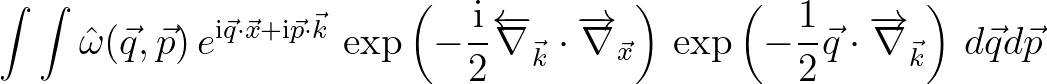

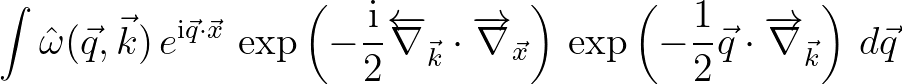
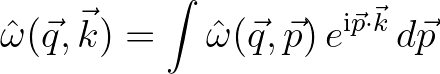 (2.221)
(2.221)
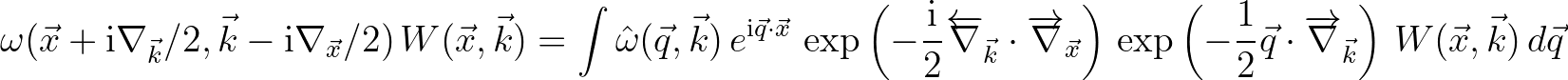 (2.222)
(2.222)
 still holds and that the term
still holds and that the term
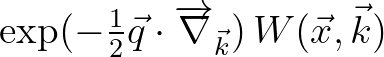 equals
the Taylor series of
equals
the Taylor series of
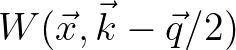 , the phase-space equation is given by
, the phase-space equation is given by
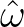 and
and 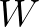 (including their derivatives).
Eq. (2.224) is the central result of the paper of Smit and Janssen (2013) (see their Eq. (15). But see also Akrish et al. (2020), their Eq. (2.19), where the mean currents have been included.)
By virtue of the assumption
(including their derivatives).
Eq. (2.224) is the central result of the paper of Smit and Janssen (2013) (see their Eq. (15). But see also Akrish et al. (2020), their Eq. (2.19), where the mean currents have been included.)
By virtue of the assumption  , they refer to this approximation as the (first order) quasi-coherent (QC) approximation.
, they refer to this approximation as the (first order) quasi-coherent (QC) approximation.
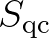 is a scattering source term that accounts for the generation and propagation of inhomogeneous wave field induced by medium variations, including wave
refraction, Doppler shifting2.11 and wave interference.
is a scattering source term that accounts for the generation and propagation of inhomogeneous wave field induced by medium variations, including wave
refraction, Doppler shifting2.11 and wave interference.
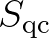 that can be efficiently computed; it is denoted by
that can be efficiently computed; it is denoted by
 .
We consider a point
.
We consider a point
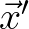 in the neighborhood of the origin.
Then let
in the neighborhood of the origin.
Then let
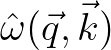 be the Fourier transform of
be the Fourier transform of
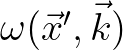 , as follows
, as follows
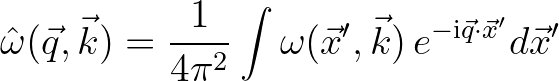 (2.225)
(2.225)
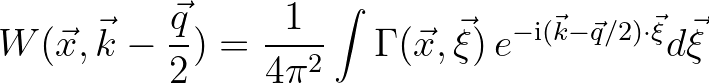 (2.226)
(2.226)
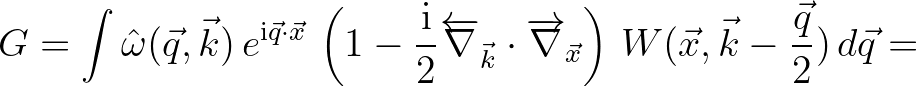
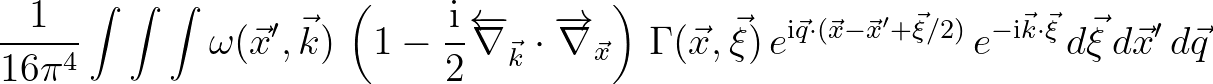
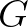

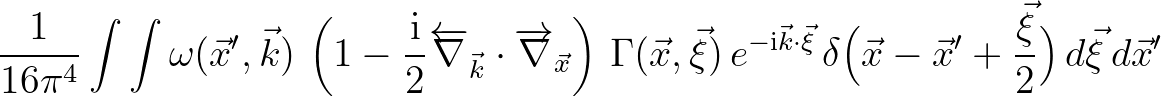

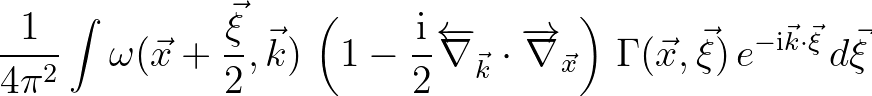
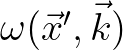 must have a compact support in
must have a compact support in
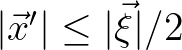 .
Since, by nature, the correlation function is compactly supported,
that is,
.
Since, by nature, the correlation function is compactly supported,
that is,
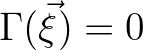 for
for
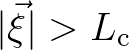 (note
(note
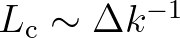 is finite), it is concluded that
the local wave statistics can only be affected by the medium within a radius
is finite), it is concluded that
the local wave statistics can only be affected by the medium within a radius 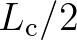 around point
around point  .
.
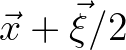 is expressed as a superposition of the local value at
is expressed as a superposition of the local value at  and a remainder,
and a remainder,
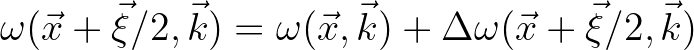 .
Then substitution gives
.
Then substitution gives

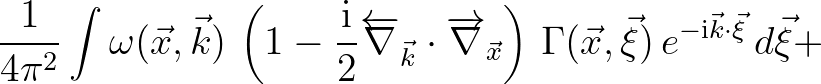
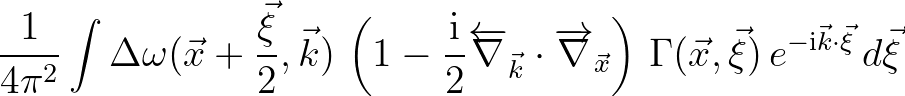

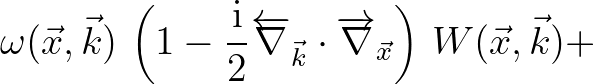
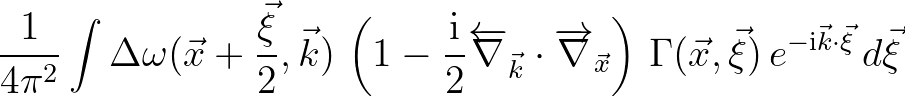
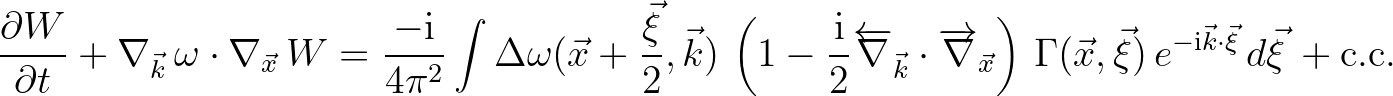 (2.227)
(2.227)
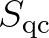

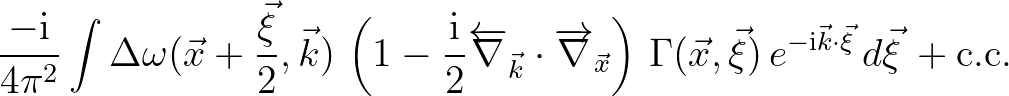

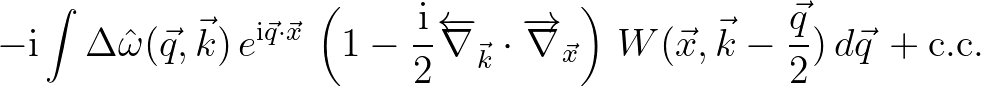
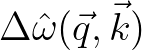 the Fourier transform of
the Fourier transform of
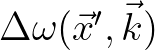 .
By shifting the origin to the point
.
By shifting the origin to the point  , the Fourier transform of
, the Fourier transform of
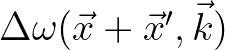 is then given by
is then given by
 (2.228)
(2.228)
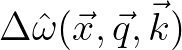 and is computed over a square domain with a fixed size
and is computed over a square domain with a fixed size 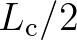 around the point
around the point  .
It should be noted that the source term
.
It should be noted that the source term 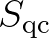 is evaluated by means of integration over
is evaluated by means of integration over 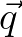 and not over
and not over 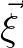 .
.