Next: The QC approximation Up: Quasi-coherent modelling Previous: The Wigner distribution
The aim of this section is the derivation of the evolution equation for the Wigner distribution. This equation governs the wave field that is considered as a phase-space representation,
that is, a description of the wave as a function of both position  and wave number
and wave number 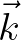 . The key to the approach to follow is the back and forth Fourier transformation between
the physical space
. The key to the approach to follow is the back and forth Fourier transformation between
the physical space  and the phase space
and the phase space
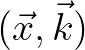 and the underlying formalism is Weyl symbol calculus (Weyl, 1931; McDonald, 1988; Cohen, 2012).
Basically, we have ordinary functions living in phase space called symbols and operators or kernels acting in physical space. The correspondence between symbols and operators
was introduced by Weyl (1931) and appeared to be useful in deriving an equation governing the phase-space representation of the wave field.
and the underlying formalism is Weyl symbol calculus (Weyl, 1931; McDonald, 1988; Cohen, 2012).
Basically, we have ordinary functions living in phase space called symbols and operators or kernels acting in physical space. The correspondence between symbols and operators
was introduced by Weyl (1931) and appeared to be useful in deriving an equation governing the phase-space representation of the wave field.
Before proceeding let us recall the following property of the Fourier transforms which will be used frequently later on.
The Fourier transform of a derivative yields the Fourier transform of the function itself multiplied by the Fourier variable.
For instance, the Fourier transform of
 is given by
is given by
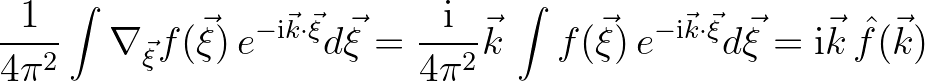 (2.201)
(2.201)
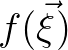 and
and
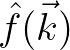 is a compactly supported smooth function and its Fourier transform, respectively.
Here, we say that the derivative
is a compactly supported smooth function and its Fourier transform, respectively.
Here, we say that the derivative
 is associated with
is associated with
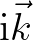 , denoted by
, denoted by
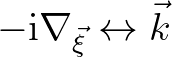 with
with
 representing
the correspondence symbol. Likewise,
representing
the correspondence symbol. Likewise,
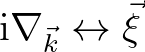 .
.
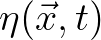 is the complex-valued surface elevation2.6and
is the complex-valued surface elevation2.6and
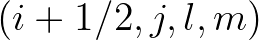 is the linear pseudo-differential wave operator associated with the dispersion relation
is the linear pseudo-differential wave operator associated with the dispersion relation
 which
is given by2.7
which
is given by2.7
 the water depth and
the water depth and
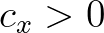 the mean current.
Eq. (2.203) is valid for linear waves propagating over slowly varying medium for which the local dispersion relation (2.204) can be employed.
the mean current.
Eq. (2.203) is valid for linear waves propagating over slowly varying medium for which the local dispersion relation (2.204) can be employed.
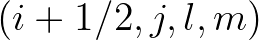 is the coordinate space representation of the operator that acts on functions living in physical space, we
invoke the Weyl rule to obtain the correspondence with phase-space functions.
This rule thus assigns operators acting on physical space to functions defined on the phase space (Cohen, 2012).
First, we define the Fourier transform of
is the coordinate space representation of the operator that acts on functions living in physical space, we
invoke the Weyl rule to obtain the correspondence with phase-space functions.
This rule thus assigns operators acting on physical space to functions defined on the phase space (Cohen, 2012).
First, we define the Fourier transform of
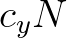 by
by
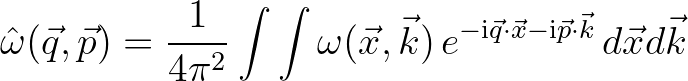 (2.204)
(2.204)
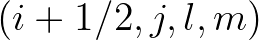 associated with
associated with
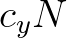 is defined by the substitution of the operator
is defined by the substitution of the operator
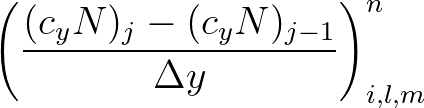 for
for
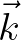 in Eq. (2.206),
in Eq. (2.206),
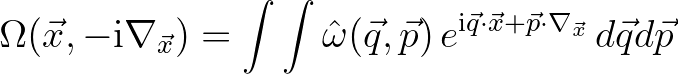 (2.206)
(2.206)
 corresponding to the operator
corresponding to the operator  the Weyl symbol of
the Weyl symbol of  ; notation: symb
; notation: symb
 = \omega(\vec{x},\vec{k})$](img726.png) .
Note further that the exponential function here is to be understood as its Taylor series expansion, that is,
.
Note further that the exponential function here is to be understood as its Taylor series expansion, that is,
![$\displaystyle e^{{\rm i}\vec{q}\cdot\vec{x}+\vec{p}\cdot\nabla_{\vec{x}}} = \su...
...{n!} \Bigl [ {\rm i}\vec{q}\cdot\vec{x}+\vec{p}\cdot\nabla_{\vec{x}} \Bigr ]^n
$](img727.png) (2.207)
(2.207)
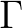 lives on the physical space. Hence, in the context of symbol formalism and considering Eq. (2.196),
lives on the physical space. Hence, in the context of symbol formalism and considering Eq. (2.196),
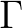 is interpreted as a coordinate space (kernel) operator and its Weyl symbol is the Wigner distribution (McDonald, 1988).
is interpreted as a coordinate space (kernel) operator and its Weyl symbol is the Wigner distribution (McDonald, 1988).
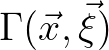 and derive its evolution equation as follows. First, referring to Eq. (2.195), we
have2.8
and derive its evolution equation as follows. First, referring to Eq. (2.195), we
have2.8
 (2.208)
(2.208)
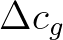 and
and
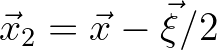 . Next, we substitute Eq. (2.203) into the above equation, resulting in
. Next, we substitute Eq. (2.203) into the above equation, resulting in
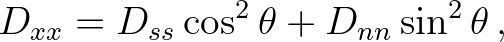 (2.209)
(2.209)
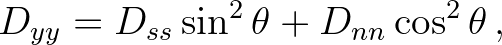 (using the inverse of the Jacobian gives
(using the inverse of the Jacobian gives
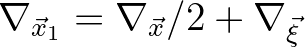 and
and
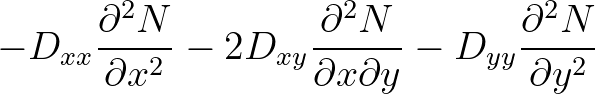 ), one obtains
), one obtains
![$\displaystyle \frac{\partial \Gamma}{\partial t}(\vec{x},\vec{\xi}) = -{\rm i} ...
...{x}}/2 - {\rm i}\nabla_{\vec{\xi}} \right ) \right ] \Gamma(\vec{x},\vec{\xi})
$](img736.png) (2.210)
(2.210)
 = W(\vec{x},\vec{k})$](img737.png) ,
the phase-space equation for the Wigner distribution can be found using the Fourier transformation, and is given by
,
the phase-space equation for the Wigner distribution can be found using the Fourier transformation, and is given by
![$\displaystyle \frac{\partial W}{\partial t}(\vec{x},\vec{k}) = -{\rm i} \left [...
...c{k}}/2,\vec{k}+{\rm i}\nabla_{\vec{x}}/2 \right ) \right ] W(\vec{x},\vec{k})
$](img738.png) (2.211)
(2.211)
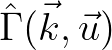 ,
and subsequently an equation governing the Wigner distribution,
,
and subsequently an equation governing the Wigner distribution,
![$W = {\rm symb}[{\hat \Gamma}]$](img741.png) , which is then exactly Eq. (2.213); see Smit and Janssen (2013).
, which is then exactly Eq. (2.213); see Smit and Janssen (2013).
 and
and 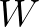 in phase space.
The purpose of what follows is to find an explicit expression for symbol
in phase space.
The purpose of what follows is to find an explicit expression for symbol
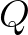 .
Its Weyl operator is given by
.
Its Weyl operator is given by
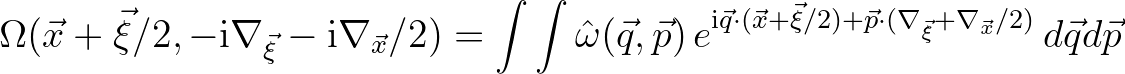 (2.213)
(2.213)
 and
and
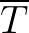 do not commute (and likewise
do not commute (and likewise
 and
and 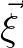 ) and their commutation relation can be expressed as
) and their commutation relation can be expressed as
![$[{\rm i}\vec{q}\cdot\vec{x},\vec{p}\cdot\nabla_{\vec{x}}/2] = -\frac{1}{2}{\rm i}\vec{q}\cdot\vec{p}$](img746.png) (and
(and
![$[\vec{p}\cdot\nabla_{\vec{\xi}},{\rm i}\vec{q}\cdot\vec{\xi}/2] = \frac{1}{2}{\rm i}\vec{p}\cdot\vec{q}$](img747.png) ).
With the aid of the Baker-Campbell-Hausdorff (BCH) identity2.9we can simplify the Weyl operator as follows
).
With the aid of the Baker-Campbell-Hausdorff (BCH) identity2.9we can simplify the Weyl operator as follows
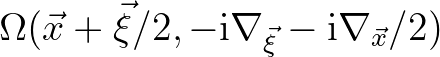 |
 |
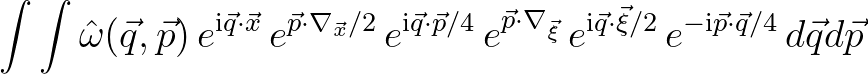 |
|
 |
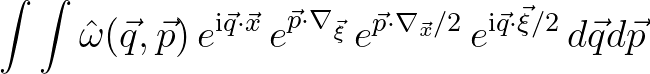 |
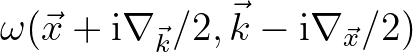 |
 |
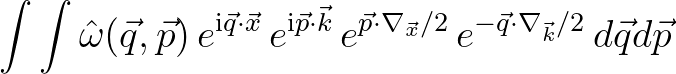 |
|
 |
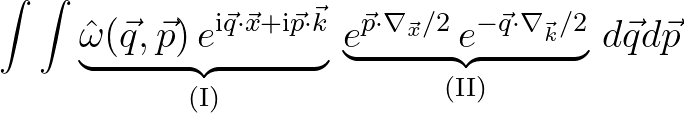 |
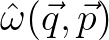 , that is, Eq. (2.206), resulting in
, that is, Eq. (2.206), resulting in
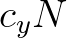 .
With respect to part (II) we recall that the exponential function can be expressed as its Taylor series, such as
.
With respect to part (II) we recall that the exponential function can be expressed as its Taylor series, such as
![$\displaystyle e^{\vec{p}\cdot\nabla_{\vec{x}}/2} = \sum_{n=0}^{\infty} \frac{1}{n!} \left [ \frac{1}{2}\vec{p}\cdot\nabla_{\vec{x}} \right ]^n
$](img758.png) (2.214)
(2.214)
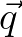 or
or 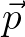 will lead to a derivative in the corresponding Fourier variable
will lead to a derivative in the corresponding Fourier variable  or
or 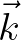 , respectively, we obtain the following
, respectively, we obtain the following
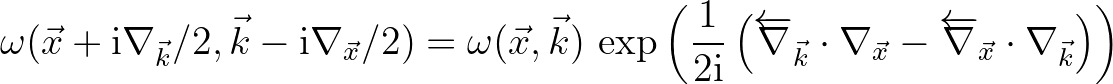 (2.215)
(2.215)
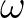 ).
Inserting in Eq. (2.213) yields
).
Inserting in Eq. (2.213) yields
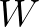 ).
The first term of the right hand side of Eq. (2.217) represents the product of the two symbols and is known as the Moyal product (Cohen, 2012).
Clearly, this product is not
commutative because the product of the associated operators in physical space is a non-commutative operator.
However, by virtue of the Weyl rule of association, the proper ordering of the arguments
).
The first term of the right hand side of Eq. (2.217) represents the product of the two symbols and is known as the Moyal product (Cohen, 2012).
Clearly, this product is not
commutative because the product of the associated operators in physical space is a non-commutative operator.
However, by virtue of the Weyl rule of association, the proper ordering of the arguments  and
and
 of operator
of operator  is obtained
such that Eq. (2.203) recasts to the correct transport equation for
is obtained
such that Eq. (2.203) recasts to the correct transport equation for
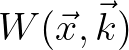 , assuming the usual WKB ansatz
(further details and discussion on this topic can be found in Smit and Janssen, 2013 and in Akrish et al., 2020).
, assuming the usual WKB ansatz
(further details and discussion on this topic can be found in Smit and Janssen, 2013 and in Akrish et al., 2020).
The SWAN team 2024-09-09