Next: The Wigner distribution Up: Governing equations Previous: Wave-induced set-up
The action balance equation (2.16) describes the evolution of the action density spectrum
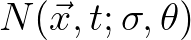 and the associated wave statistics over non-uniform bathymetry and currents, on the assumption that the wave field is Gaussian
and quasi-homogeneous. In this section we discuss a recently developed model called the Quasi-Coherent (QC) model of Smit et al. (2015a,b)
and Akrish et al. (2020) that allows for the generation and propagation of the statistically inhomogeneous wave field.
and the associated wave statistics over non-uniform bathymetry and currents, on the assumption that the wave field is Gaussian
and quasi-homogeneous. In this section we discuss a recently developed model called the Quasi-Coherent (QC) model of Smit et al. (2015a,b)
and Akrish et al. (2020) that allows for the generation and propagation of the statistically inhomogeneous wave field.
Central to the QC approach is the Wigner distribution and its evolution equation.
The underlying concept enables to describe correlation functions that combines both phase space variables, viz.  and
and 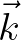 , and
has been widely adopted in, e.g. statistical mechanics, quantum mechanics and optics (Wigner, 1932; Bremmer, 1973; McDonald, 1988;
Cohen, 2012)2.3.
Below we summarize the main characteristics of the QC model. The implementation in SWAN will be dealt with in Section 3.9.
, and
has been widely adopted in, e.g. statistical mechanics, quantum mechanics and optics (Wigner, 1932; Bremmer, 1973; McDonald, 1988;
Cohen, 2012)2.3.
Below we summarize the main characteristics of the QC model. The implementation in SWAN will be dealt with in Section 3.9.