Wave-induced set-up
In a (geographic) 1D case the computation of the wave-induced set-up is based on the vertically integrated
momentum balance equation which is a balance between the wave force (gradient of the wave radiation
stress normal to the coast) and the hydrostatic pressure gradient (note that the component parallel to the
coast causes wave-induced currents but no set-up).
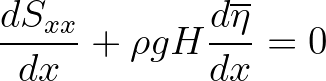 (2.185)
(2.185)
where 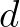 is the total water depth (including the wave-induced set-up) and
is the total water depth (including the wave-induced set-up) and 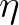 is the mean surface elevation
(including the wave-induced set-up) and
is the mean surface elevation
(including the wave-induced set-up) and
![$\displaystyle S_{xx} = \rho g \int [n \cos^2 \theta + n - \frac{1}{2}]E d \sigma d\theta
$](img669.png) (2.186)
(2.186)
is the radiation stress tensor.
Observation and computations based on the vertically integrated momentum balance equation of
Dingemans et al. (1987) show that the wave-induced currents are mainly driven by the divergence-free
part of the wave forces whereas the set-up is mainly due to the rotation-free part of these forces. To
compute the set-up in 2D, it would then be sufficient to consider the divergence of the momentum balance
equation. If the divergence of the acceleration in the resulting equation is ignored, the result is:
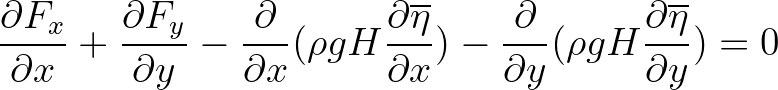 (2.187)
(2.187)
This approximation can only be applied to open coast (unlimited supply of water from outside
the domain, e.g. nearshore coasts and estuaries) in contrast to closed basin, e.g. lakes, where this approach
should not be used.
The SWAN team 2024-09-09
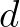 is the total water depth (including the wave-induced set-up) and
is the total water depth (including the wave-induced set-up) and 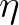 is the mean surface elevation
(including the wave-induced set-up) and
is the mean surface elevation
(including the wave-induced set-up) and