Parallel implementation aspects

Domain decomposition methods have been successfully used for solving large sparse systems arising from finite difference or finite volume methods in computational fluid dynamics on distributed memory platforms. They are based, in essence, upon a partition of the whole computational domain in 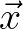$\vec{x}$-space into a number of contiguous, non-overlapping subdomains with each of them being assigned to a different processor. In this case the same algorithm performs on all available processors and on its own set of data (known as the SPMD programming model). Each subdomain can have multiple neighbors on each of its four sides. For this, a data structure is implemented to store all the information about the relationship of the subdomain and its particular neighbors. Next, each subdomain, look in isolation, is then surrounded by an auxiliary layer of one to three grid points originating from neighbouring subdomains. This layer is used to store the so-called halo data from neighbouring subdomains that are needed for the solution within the subdomain in question. The choice of one, two or three grid points depends on the use of propagation scheme in geographical space, i.e., respectively, BSBT, SORDUP or Stelling/Leendertse. Since, each processor needs data that resides in other neighbouring subdomains, exchange of data across boundaries of subdomains is necessary. Moreover, to evaluate the stopping criterion (3.37), global communication is required. These message passings are implemented by a high level communication library such as MPI standard. A popular distribution is MPICH which is free software^7.1 and is used in the present study. Only simple point-to-point and collective communications have been employed. There are, however, some other implementation and algorithmic issues that need to be addressed.