Parallelization of implicit propagation schemes
Contrary to explicit schemes, implicit ones are more difficult to parallelize, because of
the coupling introduced at subdomain interfaces. For example, concerning the four-sweep
technique, during the first sweep, an update of 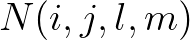 can be carried out as soon as
can be carried out as soon as
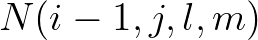 and
and 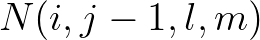 have been updated and thus it can not be performed in
parallel. Parallelization of this implicit scheme requires modifications. Ideally, the
parallel algorithm need no more computing operations than the sequential one for the same
accuracy.
have been updated and thus it can not be performed in
parallel. Parallelization of this implicit scheme requires modifications. Ideally, the
parallel algorithm need no more computing operations than the sequential one for the same
accuracy.
The simplest strategy to circumvent this problem consists in treating the data on subdomain
interfaces explicitly, which in mathematical terms amounts to using a block Jacobi
approximation of the implicit operator. In this context, we employ the RCB partition method,
since it gives the required balanced, low-communication partitioning. This strategy possess
a high degree of parallelism, but may lead to a certain degradation of convergence properties.
However, this numerical overhead can be reduced by colouring the subdomains with four different
colors and subsequently permuting the numbering of unknowns in four sweeps in accordance with
the color of subdomains. Furthermore, each subdomain is surrounded by subblocks of different
colors. See Figure 7.1. As a result, each coloured subdomain start with a different
Figure 7.1:
Four types of subblocks (red, yellow, green and black) treated differently
with respect to the ordering of updates (indicated by arrows) per sweep.
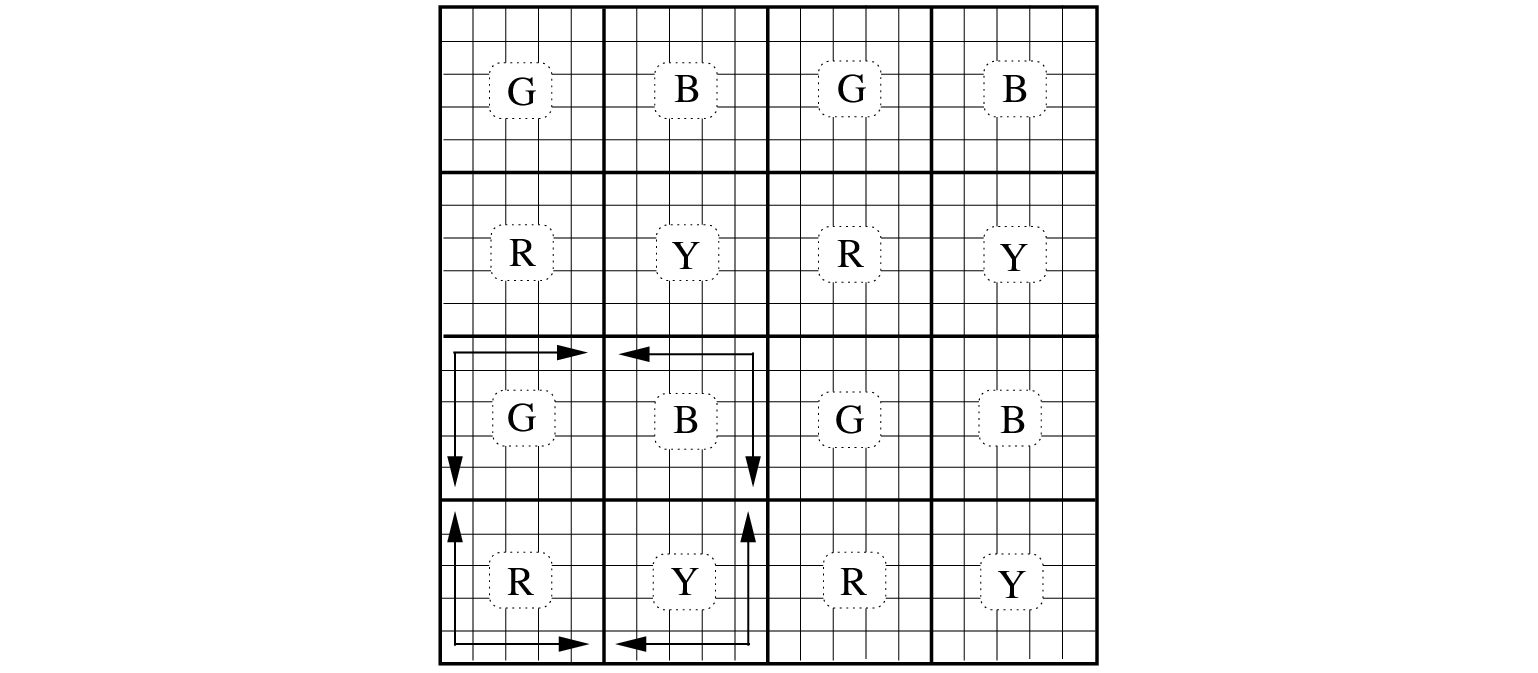 |
ordering of updates within the same sweep and thus reducing the number of synchronization
points. This multicolor ordering technique has been proposed earlier, e.g. in Meurant (1988)
and Van der Vorst (1989).
Another strategy is based on the ideas proposed by Bastian and Horton (1991) and is
referred here to as the block wavefront approach. It is demonstrated with the following
example. First, we decompose the computational domain into a number of strips. In this
example, we assume that these strips are parallel to 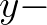 axis. Next, we start with the
first sweep. The processor belonging to the first strip updates the unknowns
axis. Next, we start with the
first sweep. The processor belonging to the first strip updates the unknowns 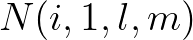 along the first row
along the first row 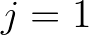 . Thereafter, communication takes place between this processor and
processor for strip 2. The unknowns
. Thereafter, communication takes place between this processor and
processor for strip 2. The unknowns 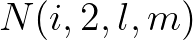 along
along 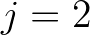 in strip 1 and
in strip 1 and 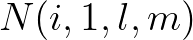 along
along
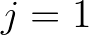 in strip 2 can be updated in parallel, and so on. After some start-up time all processors
are busy. This is depicted in Figure 7.2. Finally, this process is repeated
in strip 2 can be updated in parallel, and so on. After some start-up time all processors
are busy. This is depicted in Figure 7.2. Finally, this process is repeated
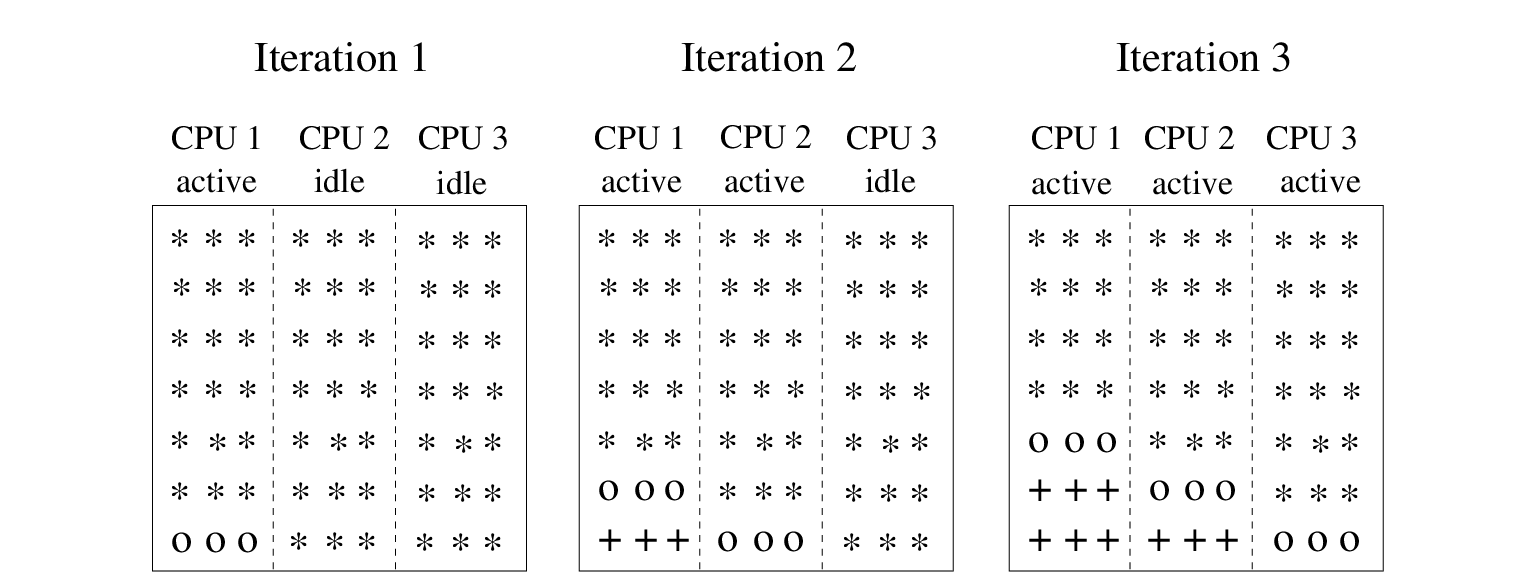
Figure 7.2:
Application of block wavefront approach for the first 3 iterations during the
first sweep. Domain is divided into 3 vertical strips. Stars represent unknowns
to be updated, circles mean that unknowns are currently updated and the plus
signs indicate unknowns that have been updated.
 |
for the other three sweeps. Details can be found in the source code of SWAN. The block
wavefront approach does not alter the order of computing operations of the sequential algorithm
and thus preserving the convergence properties, but reduces parallel efficiency to a lesser
extent because of the serial start-up and shut-down phases (Amdahl's law). This technique
resembles much to the standard wavefront technique applied in a pointwise manner (unknowns on
a diagonal are mutually independent and thus can be updated in parallel; for details, see
Templates (1994), which has also been employed by Campbell et al. (2002) for
parallelizing SWAN using OpenMP.
The performance of the two discussed parallelization methods applied in the SWAN model has been
discussed in (Zijlema, 2005).
Numerical experiments have been run on a dedicated Beowulf cluster with a real-life application.
They show that good speedups have been achieved with the
block wavefront approach, as long as the computational domain is not divided into too thin slices. Moreover,
it appears that this technique is sufficiently scalable. Concerning the block Jacobi method, a considerable
decline in performance has been observed which is attributable to the numerical overhead arising from doubling
the number of iterations due to the relative weak stopping criteria as described in Section 3.3.
Furthermore, it may result in a solution that is computed to an accuracy that may not
be realistic. In conclusion, parallelization with the block wavefront technique has been favoured and has been
implemented in the current operational version of SWAN.
Since version 41.10, it is possible to employ the block Jacobi approach instead of the wavefront technique
as an alternative (see the Implementation Manual how to
activate this approach). The user is however advised to apply the curvature-based termination criterion, as described
in Section 3.4. This will enhance the scalability significantly. This is especially the case when the user
runs a (quasi-)nonstationary simulation.
A survey of other alternatives to the parallelization of the implicit schemes is given in Templates (1994).
The SWAN team 2024-09-09
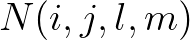 can be carried out as soon as
can be carried out as soon as
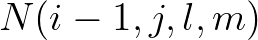 and
and 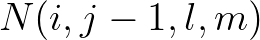 have been updated and thus it can not be performed in
parallel. Parallelization of this implicit scheme requires modifications. Ideally, the
parallel algorithm need no more computing operations than the sequential one for the same
accuracy.
have been updated and thus it can not be performed in
parallel. Parallelization of this implicit scheme requires modifications. Ideally, the
parallel algorithm need no more computing operations than the sequential one for the same
accuracy.

 axis. Next, we start with the
first sweep. The processor belonging to the first strip updates the unknowns
axis. Next, we start with the
first sweep. The processor belonging to the first strip updates the unknowns 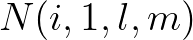 along the first row
along the first row 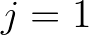 . Thereafter, communication takes place between this processor and
processor for strip 2. The unknowns
. Thereafter, communication takes place between this processor and
processor for strip 2. The unknowns 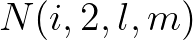 along
along 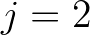 in strip 1 and
in strip 1 and 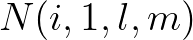 along
along
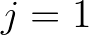 in strip 2 can be updated in parallel, and so on. After some start-up time all processors
are busy. This is depicted in Figure 7.2. Finally, this process is repeated
in strip 2 can be updated in parallel, and so on. After some start-up time all processors
are busy. This is depicted in Figure 7.2. Finally, this process is repeated
