Next: The influence of ambient Up: Sources and sinks Previous: Bragg scattering
The source term 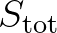 for the first- and second-generation formulation (relaxation model) of
SWAN is (Holthuijsen and de Boer, 1988):
for the first- and second-generation formulation (relaxation model) of
SWAN is (Holthuijsen and de Boer, 1988):
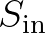 and
and 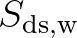 represent input by wind and decay for over-developed sea states,
respectively,
represent input by wind and decay for over-developed sea states,
respectively, 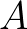 and
and 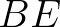 are a linear and exponential growth term, respectively,
are a linear and exponential growth term, respectively, 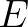 is the
spectral density,
is the
spectral density, 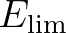 is the saturated spectrum,
is the saturated spectrum, 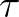 is a time scale and
is a time scale and 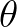 and
and
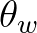 are the discrete spectral wave direction and the wind direction, respectively.
The expressions for the source terms
are the discrete spectral wave direction and the wind direction, respectively.
The expressions for the source terms 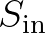 and
and 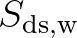 have been modified for shallow water applications
(N. Booij and L.H. Holthuijsen, personal communication, 1996) and are given below.
have been modified for shallow water applications
(N. Booij and L.H. Holthuijsen, personal communication, 1996) and are given below.
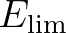 as outlined below.
as outlined below.
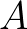 is given by an expression due to Cavaleri and Malanotte-Rizolli
(1981) as adapted by Holthuijsen and de Boer (1988) and Holthuijsen et al. (1996):
is given by an expression due to Cavaleri and Malanotte-Rizolli
(1981) as adapted by Holthuijsen and de Boer (1988) and Holthuijsen et al. (1996):
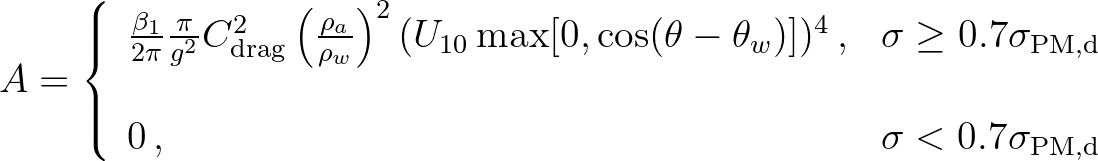 (2.159)
(2.159)
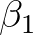 is a coefficient that has been tuned to be
is a coefficient that has been tuned to be 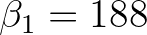 ,
,
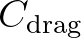 is a drag coefficient equal to
is a drag coefficient equal to
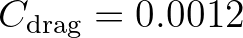 and
and
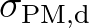 is the fully developed peak frequency including the effect of shallow
water and is estimated from the depth dependent
relation of the Shore Protection Manual (1973):
is the fully developed peak frequency including the effect of shallow
water and is estimated from the depth dependent
relation of the Shore Protection Manual (1973):
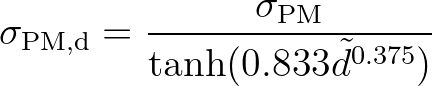 (2.160)
(2.160)
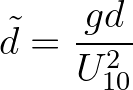 (2.161)
(2.161)
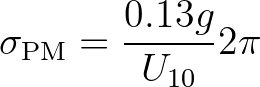 (2.162)
(2.162)
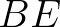 is due to Snyder et al. (1981) rescaled in terms of
is due to Snyder et al. (1981) rescaled in terms of 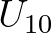 as
adapted by Holthuijsen and de Boer (1988) and Holthuijsen et al. (1996):
as
adapted by Holthuijsen and de Boer (1988) and Holthuijsen et al. (1996):
![$\displaystyle B = \max [0, \beta_2 \frac{5}{2\pi} \frac{\rho_a}{\rho_w} (\frac{U_{10}}{\sigma/k}\cos(\theta-\theta_w) -\beta_3)]\sigma
$](img605.png) (2.163)
(2.163)
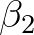 and
and 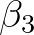 have been tuned to be
have been tuned to be
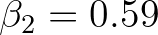 and
and
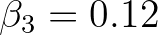 .
.
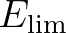 , (e.g.,
when the wind decreases), energy is dissipated with a relaxation model:
, (e.g.,
when the wind decreases), energy is dissipated with a relaxation model:
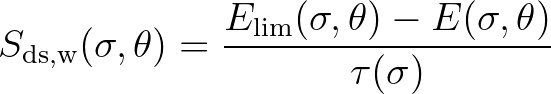 (2.164)
(2.164)
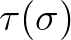 is a time scale given by
is a time scale given by
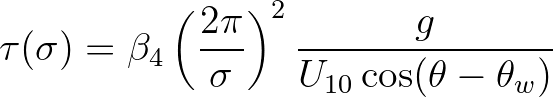 (2.165)
(2.165)
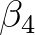 has been tuned to be
has been tuned to be 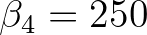 .
.
 directional
distribution centred at the local wind direction
directional
distribution centred at the local wind direction 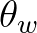 . It is essentially an adapted
Pierson-Moskowitz (1964) spectrum:
. It is essentially an adapted
Pierson-Moskowitz (1964) spectrum:
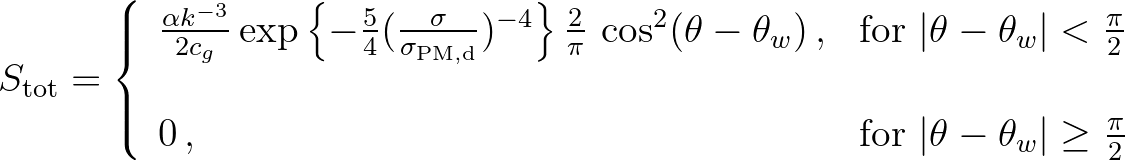 (2.166)
(2.166)
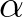 is a constant and equals
is a constant and equals
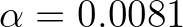 (2.167)
(2.167)
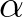 depends on the total dimensionless
wave energy
depends on the total dimensionless
wave energy
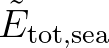 of the wind sea part of the spectrum and the dimensionless depth
of the wind sea part of the spectrum and the dimensionless depth 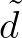 :
:
![$\displaystyle \alpha = \max [ (0.0081 + (0.013 - 0.0081)e^{-{\tilde d}}), 0.0023 {\tilde E}^{-0.223}_{\rm tot,sea} ]
$](img620.png) (2.168)
(2.168)
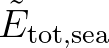 is given by
is given by
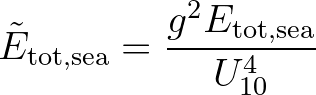 (2.169)
(2.169)
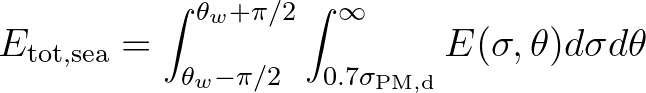 (2.170)
(2.170)
 is taken to be 0.155. This dependency of
is taken to be 0.155. This dependency of  on the local
dimensionless energy of the wind sea permits an overshoot in the wave spectrum under wave
generation conditions. For deep water
on the local
dimensionless energy of the wind sea permits an overshoot in the wave spectrum under wave
generation conditions. For deep water
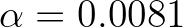 as proposed by Pierson and Moskowitz (1964).
as proposed by Pierson and Moskowitz (1964).
The SWAN team 2024-09-09