Next: First- and second-generation model Up: Sources and sinks Previous: Wave damping due to
As waves propagate from deep towards shallow water they interact with the seabed. Because of the large scale variations of the bottom topography
(at the scale of many tens or hundreds of wave lengths), waves tend to shoal and refract towards the coast. On the other hand, irregular bed variations at
shorter scales (i.e. within a few wave lengths) result in forward and backward scattering of waves, known as the Bragg scattering. In general,
forward scattering counteracts the directional narrowing caused by refraction and leads to a broadening of the directional spreading,
whereas backward scattering attenuates the incident wave field (Ardhuin et al., 2003).
Ardhuin and Herbers (2002) developed a theory for the Bragg scattering of surface waves and proposed a source term that can be implemented in spectral wave models.
This source term describes the lowest order resonant interaction between a triad of two wave components with the same frequency but different wave number vectors
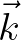 and
and 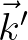 (and thus the associated directions
(and thus the associated directions 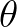 and
and 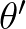 ), and a bottom component that has the difference wave number
), and a bottom component that has the difference wave number
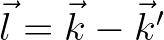 .
This source term is given by
.
This source term is given by
![$\displaystyle S_{\rm bragg} (\sigma,\theta) = \chi\, \int_0^{2\pi}\, \cos^2(\th...
...iny B}(\vec{l}) \left [ E(\sigma,\theta') - E(\sigma,\theta) \right ] d\theta'
$](img582.png) (2.156)
(2.156)
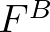 is the bed elevation spectrum representing the random (small-scale) variability of the seabed, and
is the bed elevation spectrum representing the random (small-scale) variability of the seabed, and 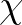 is the coupling coefficient and is expressed as follows
is the coupling coefficient and is expressed as follows
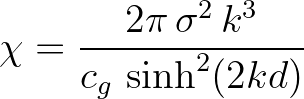 (2.157)
(2.157)
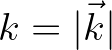 . (Note that in contrast to the study of Ardhuin and Herbers (2002), the present source term is formulated in
. (Note that in contrast to the study of Ardhuin and Herbers (2002), the present source term is formulated in
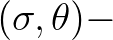 space.)
space.)
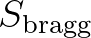 is estimated by means of a bottom spectrum
is estimated by means of a bottom spectrum 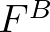 at the difference wave number
at the difference wave number 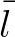 . In SWAN, two options are available to input this
spectrum.
. In SWAN, two options are available to input this
spectrum.
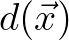 given at the computational grid points, so that refraction is
resolved properly. The remainder, that is, the small-scale bed modulation, is used to compute the bottom spectrum
given at the computational grid points, so that refraction is
resolved properly. The remainder, that is, the small-scale bed modulation, is used to compute the bottom spectrum 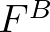 based on a Fourier transform from
based on a Fourier transform from  to
to 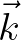 .
.
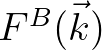 is assumed to be obtained elsewhere and is the same at all computational grid points. Furthermore, the inputted
bathymetry
is assumed to be obtained elsewhere and is the same at all computational grid points. Furthermore, the inputted
bathymetry 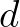 may vary on a scale at which refraction is dominant.
may vary on a scale at which refraction is dominant.
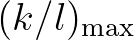 , displaying the ratio between surface and bed elevation wave numbers with
, displaying the ratio between surface and bed elevation wave numbers with  , is set to 5 (Ardhuin and Herbers, 2002).
, is set to 5 (Ardhuin and Herbers, 2002).
The SWAN team 2024-09-09