Next: Bragg scattering Up: Sources and sinks Previous: Wave damping due to
SWAN has an option to include wave dissipation by sea ice. Sea ice has two effects, direct and indirect.
A direct dissipation of wave energy occurs due to the presence of sea ice. This dissipation is represented in SWAN using empirical formula.
The temporal exponential decay rate of energy is
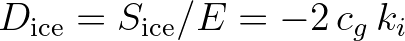 (2.152)
(2.152)
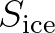 is the sea ice sink term, and
is the sea ice sink term, and 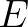 is the wave energy spectrum. Here,
is the wave energy spectrum. Here, 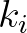 (in 1/m) is the linear exponential attenuation rate of wave amplitude in space,
(in 1/m) is the linear exponential attenuation rate of wave amplitude in space,
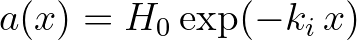 . The factor 2 above provides a conversion from amplitude decay to energy decay. The group velocity
. The factor 2 above provides a conversion from amplitude decay to energy decay. The group velocity 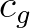 provides conversion from spatial decay
to temporal decay.
provides conversion from spatial decay
to temporal decay. 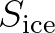 and
and 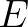 vary with frequency and direction.
vary with frequency and direction.
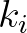 may vary with frequency
according to
may vary with frequency
according to
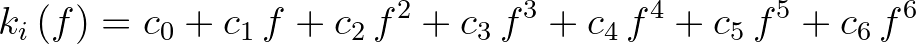 (2.153)
(2.153)
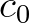 to
to 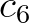 the user-defined polynomial coefficients. These coefficients are dimensional; e.g.
the user-defined polynomial coefficients. These coefficients are dimensional; e.g. 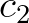 has units of s
has units of s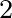 /m.
/m.
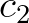 =1.06
=1.06 10
10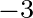 s
s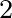 /m and
/m and 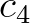 =2.3
=2.3 10
10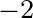 s
s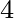 /m. This recovers
the polynomial of Meylan et al. (2014), calibrated for a case of ice floes, mostly 10 to 25 m in
diameter, in the marginal ice zone near Antarctica. Another calibration, for a case that is similar
except with relatively thinner ice, from Rogers et al. (2021a) is
/m. This recovers
the polynomial of Meylan et al. (2014), calibrated for a case of ice floes, mostly 10 to 25 m in
diameter, in the marginal ice zone near Antarctica. Another calibration, for a case that is similar
except with relatively thinner ice, from Rogers et al. (2021a) is 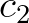 =0.208
=0.208 10
10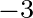 s
s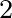 /m and
/m and
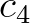 =5.18
=5.18 10
10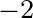 s
s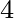 /m. Other polynomials are provided in Rogers et al. (2018). An example is for a case of
pancake and frazil ice:
/m. Other polynomials are provided in Rogers et al. (2018). An example is for a case of
pancake and frazil ice: 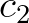 =0.284
=0.284 10
10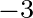 s
s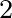 /m and
/m and 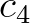 =1.53
=1.53 10
10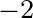 s
s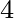 /m.
/m.
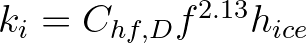 ,
with default
,
with default 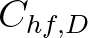 = 0.1 based on the same study, for pancake ice in the marginal ice zone (MIZ)
of the Weddell Sea (Antarctica).
= 0.1 based on the same study, for pancake ice in the marginal ice zone (MIZ)
of the Weddell Sea (Antarctica).
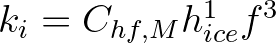 , where
, where 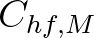 includes a viscosity
parameter. Our implementation here has a default
includes a viscosity
parameter. Our implementation here has a default
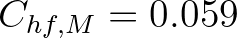 based on calibration to the Rogers
et al. (2021a) dataset (broken floes in the Antarctic MIZ) by Rogers et al. (2021b). Two earlier
calibrations were performed by Liu et al. (2020):
based on calibration to the Rogers
et al. (2021a) dataset (broken floes in the Antarctic MIZ) by Rogers et al. (2021b). Two earlier
calibrations were performed by Liu et al. (2020):
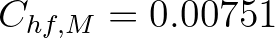 for a case of broken floes in the
Antarctic MIZ and
for a case of broken floes in the
Antarctic MIZ and
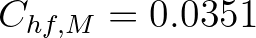 for a case of pancake and frazil ice near the Beaufort Sea.
for a case of pancake and frazil ice near the Beaufort Sea.
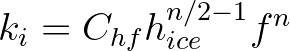 . Those authors calibrate it to the dataset of
Rogers et al. (2021a), giving
. Those authors calibrate it to the dataset of
Rogers et al. (2021a), giving 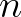 = 4.5 and
= 4.5 and 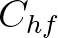 = 2.9.
= 2.9.
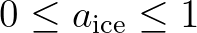 .
The effect on wind input is a scaling of the wind input source functions by open water fraction
.
The effect on wind input is a scaling of the wind input source functions by open water fraction 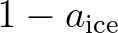 ,
,
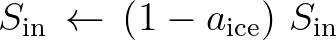 (2.154)
(2.154)
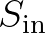 the wind input term; see Eq. (2.33).
This effect can be reduced or disabled (see command SET [icewind].)
the wind input term; see Eq. (2.33).
This effect can be reduced or disabled (see command SET [icewind].)
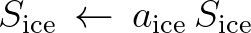 (2.155)
(2.155)
The SWAN team 2024-09-09