Problem definition
The equation to be solved has the following form:
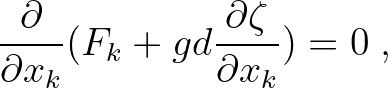 (5.4)
(5.4)
In order to solve (5.4), the following types of boundary conditions
may be applied
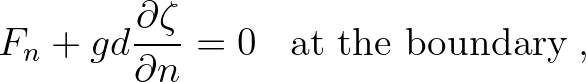 (5.5)
(5.5)
with 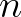 the outward direct normal. This is a Neumann condition.
The setup is fixed upon an additive constant.
the outward direct normal. This is a Neumann condition.
The setup is fixed upon an additive constant.
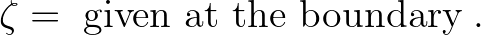 (5.6)
(5.6)
This is boundary condition of Dirichlet type.
At beaches always the Neumann condition (5.5) is applied.
In order to solve (5.4) with boundary conditions (5.5) and
(5.6) a boundary fitted, vertex centered finite volume method is
applied.
In the remainder of this Chapter we use 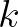 instead of
instead of 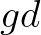 .
.
The SWAN team 2024-09-09
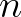 the outward direct normal. This is a Neumann condition.
The setup is fixed upon an additive constant.
the outward direct normal. This is a Neumann condition.
The setup is fixed upon an additive constant.
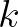 instead of
instead of 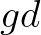 .
.