Next: Treatment of the boundary Up: Discretization of the 2D Previous: Problem definition
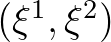 plane, which is called the computational domain. All points of
the domain are used, including the dry ones.
plane, which is called the computational domain. All points of
the domain are used, including the dry ones.
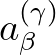 the components of the contravariant basevectors
the components of the contravariant basevectors
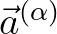 defined as
defined as
 the Jacobian of the transformation
the Jacobian of the transformation
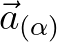 are the covariant base vectors defined by
are the covariant base vectors defined by
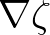 is a derivative in the Cartesian
is a derivative in the Cartesian  direction and not in the
direction and not in the 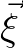 direction.
direction.
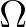 (-1,0), (0,-1), (1,0), (0,1).
(-1,0), (0,-1), (1,0), (0,1).
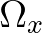 is the cell in the physical space and
is the cell in the physical space and 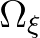 the
cell in the computational domain.
the
cell in the computational domain.
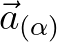 are approximated by
central differences
are approximated by
central differences
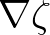 needs special attention. Since it concerns derivatives
in the
needs special attention. Since it concerns derivatives
in the 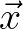 direction, whereas all derivatives in the computational
domain are in the
direction, whereas all derivatives in the computational
domain are in the 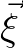 directions it is necessary to make some
approximation. We approximate this term by the integration path method
as outlined in Wesseling (2001).
directions it is necessary to make some
approximation. We approximate this term by the integration path method
as outlined in Wesseling (2001).
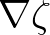 is integrated in two independent directions
is integrated in two independent directions
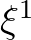 and
and 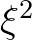 . This yields two equations to express
. This yields two equations to express
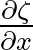 and
and
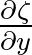 in
in
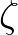 values of neighbours.
values of neighbours.
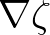 into
into 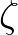 values. Solution of this linear
system results in:
values. Solution of this linear
system results in: