Treatment of the boundary conditions
The boundary conditions at the outer boundary of the domain are relatively
easy to implement.
In case of Dirichlet boundary conditions the corresponding row of the
matrix is made equal to 0 and the diagonal element is set to 1. The value
of the boundary condition is filled into the right hand side.
Neumann boundary conditions are treated integrating over a half cell as
sketched in Figure 5.2.
Figure 5.2:
Half cell at boundary
 |
In this case we get:
| |
|
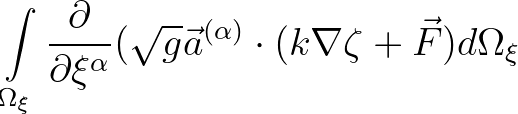 |
|
| |
|
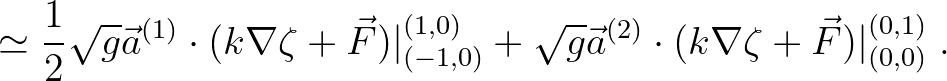 |
(5.23) |
Due to the Neumann boundary conditions the term in the boundary point (0,
0) vanishes.
Mark that in this case we need to evaluate 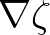 at the boundary.
In order to do so we apply a one-sided integration path approach i.e.
at the boundary.
In order to do so we apply a one-sided integration path approach i.e.
| |
|
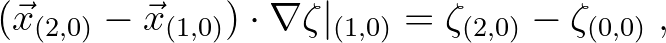 |
|
| |
|
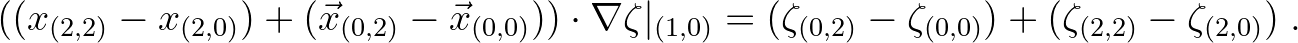 |
(5.24) |
Furthermore we need the values of
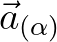 in virtual cells,
because we need the
in virtual cells,
because we need the 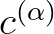 at the boundary. To that end we
construct a row of virtual cells by extrapolating the co-ordinates of the
boundary cells.
The SWAN team 2024-09-09
at the boundary. To that end we
construct a row of virtual cells by extrapolating the co-ordinates of the
boundary cells.
The SWAN team 2024-09-09
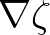 at the boundary.
In order to do so we apply a one-sided integration path approach i.e.
at the boundary.
In order to do so we apply a one-sided integration path approach i.e.
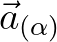 in virtual cells,
because we need the
in virtual cells,
because we need the 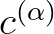 at the boundary. To that end we
construct a row of virtual cells by extrapolating the co-ordinates of the
boundary cells.
The SWAN team 2024-09-09
at the boundary. To that end we
construct a row of virtual cells by extrapolating the co-ordinates of the
boundary cells.
The SWAN team 2024-09-09