The implementation of dry points
Dry points complicate the implementation considerably.
For the dry points itself there is no problem. In fact we make the
corresponding row of the matrix, as well as the right hand side element
completely equal to zero.
Dry points in the neighbourhood of wet points, however, also influence the
matrix for the wet point. Consider for example the integration point (1,0)
in Figure 5.3.
Figure 5.3:
Dry point (2, 0) and wet point (0, 0)
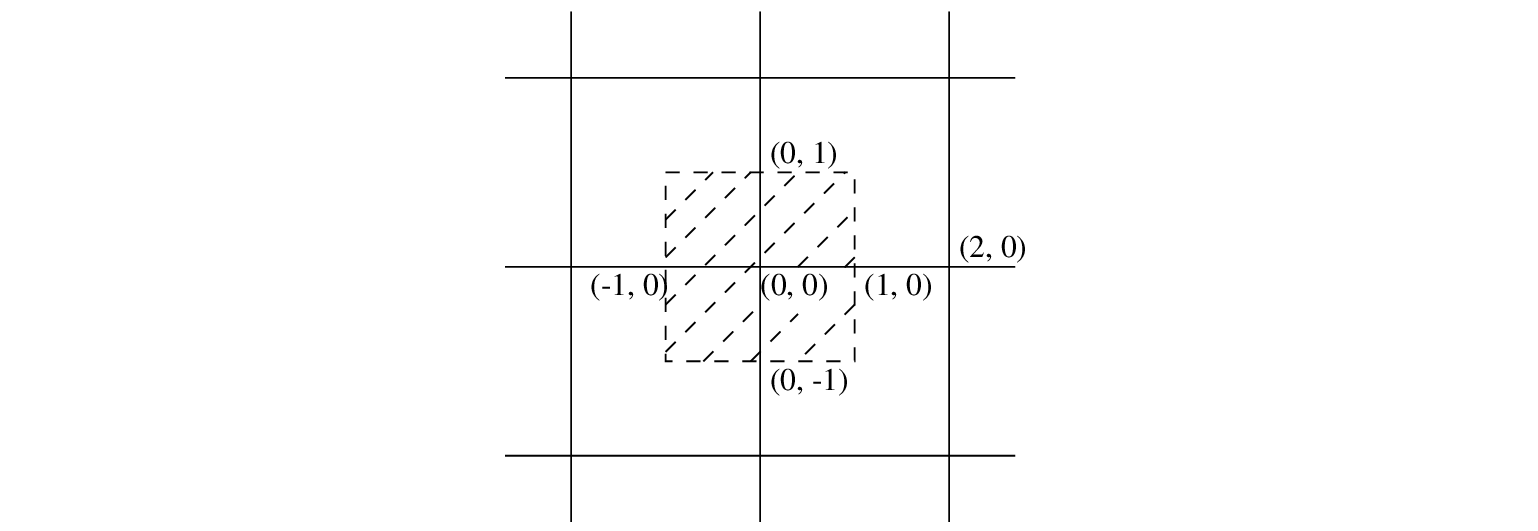 |
If (0,0) is a wet point and (2,0) a dry point then we assume that at
point (1,0) we have a Neumann boundary condition. This means in fact that
the contribution of the integration point (1,0) to the matrix and right hand
side is equal to zero. With respect to the evaluation of the gradient of
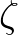 with the integration path method one sided differences are applied
for those formulas involving
with the integration path method one sided differences are applied
for those formulas involving 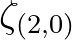 . This process is applied for
all transitions from wet to dry points. As a consequence, in the case of a
situation like in Figure 5.4 we make
. This process is applied for
all transitions from wet to dry points. As a consequence, in the case of a
situation like in Figure 5.4 we make 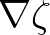 for point 2
zero.
for point 2
zero.
Figure 5.4:
Wet points  enclosed by a row of dry points
enclosed by a row of dry points 
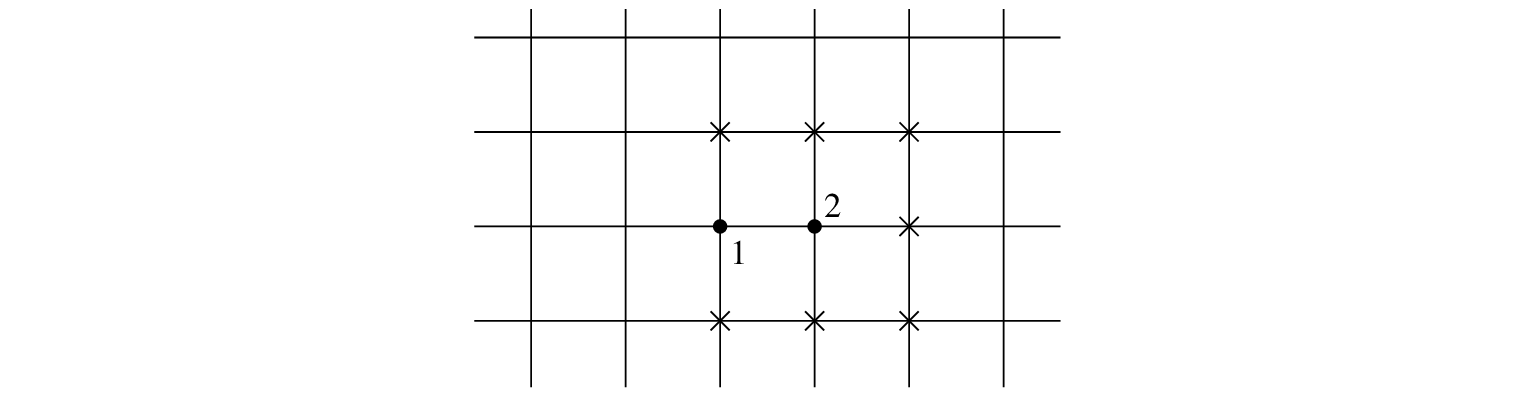 |
The reason is that in point 2 it is only possible to evaluate
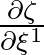 and not
and not
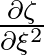 , and hence we have too few information to express
, and hence we have too few information to express
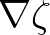 in neighbour values.
The SWAN team 2024-09-09
in neighbour values.
The SWAN team 2024-09-09
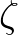 with the integration path method one sided differences are applied
for those formulas involving
with the integration path method one sided differences are applied
for those formulas involving 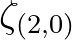 . This process is applied for
all transitions from wet to dry points. As a consequence, in the case of a
situation like in Figure 5.4 we make
. This process is applied for
all transitions from wet to dry points. As a consequence, in the case of a
situation like in Figure 5.4 we make 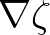 for point 2
zero.
The reason is that in point 2 it is only possible to evaluate
for point 2
zero.
The reason is that in point 2 it is only possible to evaluate
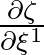 and not
and not
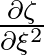 , and hence we have too few information to express
, and hence we have too few information to express
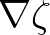 in neighbour values.
The SWAN team 2024-09-09
in neighbour values.
The SWAN team 2024-09-09