Next: Properties of the matrix Up: The iterative solver for Previous: The iterative solver for
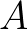 is the discrete Poisson operator,
is the discrete Poisson operator, 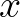 is an approximation of
the setup (of the water level), and the right hand side vector
is an approximation of
the setup (of the water level), and the right hand side vector 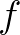 contains the effects of the boundary conditions and the forces due to
the surface waves. In the solver it is very efficient to calculate with
direct addressing, so dry points are included in the vector
contains the effects of the boundary conditions and the forces due to
the surface waves. In the solver it is very efficient to calculate with
direct addressing, so dry points are included in the vector 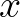 . This
implies that the dimension of
. This
implies that the dimension of 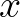 and
and 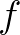 are fixed and equal to
are fixed and equal to
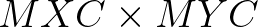 . In the discretization a 9-point stencil is used. That
implies that only 9 matrix elements per row are non-zero. These elements
are stored in a diagonal-wise way. So for this part
. In the discretization a 9-point stencil is used. That
implies that only 9 matrix elements per row are non-zero. These elements
are stored in a diagonal-wise way. So for this part 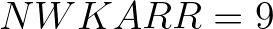 . The
rows corresponding to dry points are filled with zeroes except on the
main diagonal where the value 1 is substituted. The value of
. The
rows corresponding to dry points are filled with zeroes except on the
main diagonal where the value 1 is substituted. The value of 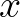 and
and 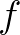 are taken equal to 0 at these points.
are taken equal to 0 at these points.