Properties of the matrix
The discrete operator is symmetric in the inner region. This means that
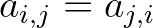 . Due to the boundary conditions the symmetry of the
operator is lost. The reasons for this are:
. Due to the boundary conditions the symmetry of the
operator is lost. The reasons for this are:
- When Dirichlet boundary conditions are used the known elements of
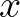 should be eliminated in order to keep the matrix symmetric. However this
leads to a different dimension of
should be eliminated in order to keep the matrix symmetric. However this
leads to a different dimension of 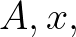 and
and 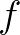 , therefore the known
elements are not eliminated.
, therefore the known
elements are not eliminated.
- When dry points occur the derivation of the discrete boundary
conditions is already complicated at the interface between wet and dry
points. At this moment it is not clear how to discretize these
conditions such that the resulting matrix is symmetric.
These difficulties motivate us to use a non-symmetric matrix. This is
only a small drawback, because recently good methods have
been developed to
solve non-symmetric matrix vector systems.
When Neumann conditions are used on all boundaries the resulting matrix
is singular. The solution is determined up to a constant. We have to
keep this in mind during the construction of the solution
procedure.
When Gauss elimination is used to solve equation (5.25), the
zero elements in the bend of 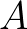 become non-zero. This means that the
required memory is equal to
become non-zero. This means that the
required memory is equal to
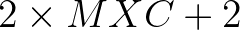 vectors.
For
vectors.
For 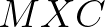 large, this leads to an unacceptable large amount of memory.
Therefore we use an iterative solution method, where the total amount of
memory is less than the memory used in the discretization procedure.
The SWAN team 2024-09-09
large, this leads to an unacceptable large amount of memory.
Therefore we use an iterative solution method, where the total amount of
memory is less than the memory used in the discretization procedure.
The SWAN team 2024-09-09
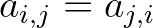 . Due to the boundary conditions the symmetry of the
operator is lost. The reasons for this are:
. Due to the boundary conditions the symmetry of the
operator is lost. The reasons for this are:
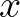 should be eliminated in order to keep the matrix symmetric. However this
leads to a different dimension of
should be eliminated in order to keep the matrix symmetric. However this
leads to a different dimension of 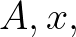 and
and 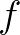 , therefore the known
elements are not eliminated.
, therefore the known
elements are not eliminated.
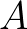 become non-zero. This means that the
required memory is equal to
become non-zero. This means that the
required memory is equal to
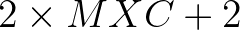 vectors.
For
vectors.
For 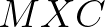 large, this leads to an unacceptable large amount of memory.
Therefore we use an iterative solution method, where the total amount of
memory is less than the memory used in the discretization procedure.
The SWAN team 2024-09-09
large, this leads to an unacceptable large amount of memory.
Therefore we use an iterative solution method, where the total amount of
memory is less than the memory used in the discretization procedure.
The SWAN team 2024-09-09