Next: Bibliography Up: Unstructured mesh implementation Previous: Calculation of diffusion-like terms
In this section, we proof that the discretization Eq. (8.16) is energy conserving. For this,
we assume stationarity and neglect the source terms, so 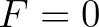 . From Eq. (8.16), it follows
. From Eq. (8.16), it follows
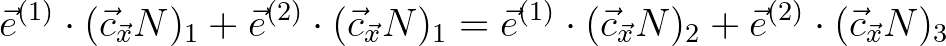 (8.40)
(8.40)
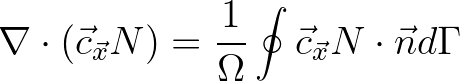 (8.41)
(8.41)
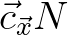 at edges are taken as averages, and so (see Figure 8.3 for reference)
at edges are taken as averages, and so (see Figure 8.3 for reference)
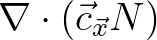 |
 |
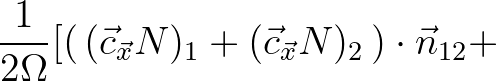 |
|
![$\displaystyle (\, (\vec{c}_{\vec{x}} N)_2 + (\vec{c}_{\vec{x}} N)_3 \,) \cdot {...
...\, (\vec{c}_{\vec{x}} N)_3 + (\vec{c}_{\vec{x}} N)_1 \,) \cdot {\vec{n}}_{31} ]$](img1503.png) |
(8.42) |
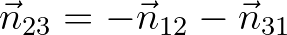 (8.43)
(8.43)
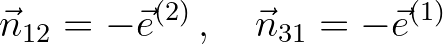 (8.44)
(8.44)
![$\displaystyle \nabla \cdot (\vec{c}_{\vec{x}} N) \approx \frac{1}{2\Omega}
[ {...
... (\vec{c}_{\vec{x}} N)_2 - {\vec{e}}^{(2)} \cdot (\vec{c}_{\vec{x}} N)_3 ] = 0
$](img1506.png) (8.45)
(8.45)
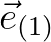 and
and 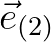 (see Figure 8.2 for reference).
The BSBT scheme is thus consistent with local wave characteristics and can be viewed as a semi-Lagrangian scheme.
This also holds for non-uniform depth and ambient current.
(see Figure 8.2 for reference).
The BSBT scheme is thus consistent with local wave characteristics and can be viewed as a semi-Lagrangian scheme.
This also holds for non-uniform depth and ambient current.
The SWAN team 2024-09-09