Next: Numerics Up: Model description Previous: Boundary and initial conditions Index
GEN1 [cf10] [cf20] [cf30] [cf40] [edmlpm] [cdrag] [umin] [cfpm]

With this command the user indicates that SWAN should run in first-generation mode (see Scientific/Technical documentation).
| [cf10] | controls the linear wave growth. | |
| Default: [cf10] = 188. | ||
| [cf20] | controls the exponential wave growth. | |
| Default: [cf20] = 0.59 | ||
| [cf30] | controls the exponential wave growth. | |
| Default: [cf30] = 0.12 | ||
| [cf40] | controls the dissipation rate, i.e., the time decay scale. | |
| Default: [cf40] = 250. | ||
| [edmlpm] | maximum non-dimensionless energy density of the wind sea part of the spectrum | |
| according to Pierson Moskowitz. | ||
| Default: [edmlpm] = 0.0036 | ||
| [cdrag] | drag coefficient. | |
| Default: [cdrag] = 0.0012 | ||
| [umin] | minimum wind velocity (relative to current; all wind speeds are taken at 10 m | |
| above sea level). | ||
| Default: [umin] = 1. | ||
| [cfpm] | coefficient which determines the Pierson Moskowitz frequency: | |
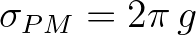 [cfpm] [cfpm] 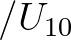 |
||
| Default: [cfpm] = 0.13 |
GEN2 [cf10] [cf20] [cf30] [cf40] [cf50] [cf60] [edmlpm] [cdrag] [umin] [cfpm]

With this command the user indicates that SWAN should run in second-generation mode (see Scientific/Technical documentation).
The variables are identical to those in the GEN1 command except that [cf50] and [cf60] are added.
| [cf50] | controls the spectral energy scale of the limit spectrum. | |
| Default: [cf50] = 0.0023 | ||
| [cf60] | controls the spectral energy scale of the limit spectrum. | |
Default: [cf60] =  0.223 0.223 |
| JANSsen [cds1] [delta] | |
| | | -> WU | |
| KOMen [cds2] [stpm] > DRAG < > |
| | | FIT | |
| -> WESTHuysen | |
| |
| ST6 [a1sds] [a2sds] [p1sds] [p2sds] & |
GEN3 < > (AGROW [a])
| | -> UP | | -> HWANG | |
| < > < FAN > VECTAU|SCATAU & |
| | DOWN | | ECMWF | |
| |
| | TRUE10 | |
| < > DEBias [cdfac] |
| | -> U10Proxy [windscaling] | |

With this command the user indicates that SWAN should run in third-generation mode for wind input, quadruplet interactions and whitecapping.
Triads, bottom friction and depth-induced breaking are not activated by this command. See also the Scientific/Technical documentation for more information.
The option GEN3 WESTH is the default. Note that SWAN converts 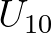 to
to 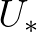 using a wind drag formula to be specified below.
using a wind drag formula to be specified below.
The choices with respect to option GEN3 ST6 are elaborated on here. Some background information on these choices can be found in Rogers et al. (2012) (henceforth denoted as RBW12).
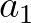 ,
, 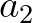 ,
,  , and
, and  , respectively, in RBW12.
The examples given below are calibrated (same method as in RBW12).
The calibration is affected by the VECTAU and U10PROXY settings. We recommend that this calibration be kept to the examples given. However, it is possible to recalibrate using the
same method as RBW12.
, respectively, in RBW12.
The examples given below are calibrated (same method as in RBW12).
The calibration is affected by the VECTAU and U10PROXY settings. We recommend that this calibration be kept to the examples given. However, it is possible to recalibrate using the
same method as RBW12.
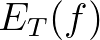 or
or 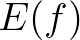 as in RBW12 (right column, page 1333).
as in RBW12 (right column, page 1333).
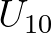 with [windscaling]
with [windscaling]
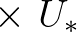 . As noted by RBW12,
Komen et al. (1984) (and so the default form of SWAN's Sds) use this approach also (with [windscaling] = 28). Increasing [windscaling] from 28 to 32 or 35 will improve prediction
of mean square slope.
. As noted by RBW12,
Komen et al. (1984) (and so the default form of SWAN's Sds) use this approach also (with [windscaling] = 28). Increasing [windscaling] from 28 to 32 or 35 will improve prediction
of mean square slope.
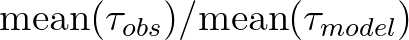 ,
where
,
where  is the wind stress, and both (observation and model, respectively, with careful attention to anemometer height when applicable) are calculated via the same formula (e.g. Hwang, 2011)
from
is the wind stress, and both (observation and model, respectively, with careful attention to anemometer height when applicable) are calculated via the same formula (e.g. Hwang, 2011)
from  . This method of selecting the wind adjustment using
. This method of selecting the wind adjustment using  (at least partially) accounts for the higher importance of high wind speeds in a wave model, making it better than an
adjustment based on simple
(at least partially) accounts for the higher importance of high wind speeds in a wave model, making it better than an
adjustment based on simple 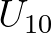 bias. If the user has not evaluated the winds, it is recommended to omit this command, or use DEB 1., which has the same effect as omitting it.
The effect of
bias. If the user has not evaluated the winds, it is recommended to omit this command, or use DEB 1., which has the same effect as omitting it.
The effect of
![$\sqrt {\mbox{\tt [cdfac]}}$](img79.png) is similar to changing the [fac] option (see command READINP) when reading in winds, though there are differences due to the
nonlinear features of the drag formula: typically small, but larger with very strong winds. Also note that using the [fac] option will modify wind field outputs from SWAN.
is similar to changing the [fac] option (see command READINP) when reading in winds, though there are differences due to the
nonlinear features of the drag formula: typically small, but larger with very strong winds. Also note that using the [fac] option will modify wind field outputs from SWAN.
GEN3 ST6 4.7E-7 6.6E-6 4.0 4.0 UP HWANG VECTAU U10PROXY 28.0 AGROW GEN3 ST6 4.7E-7 6.6E-6 4.0 4.0 UP FAN VECTAU U10PROXY 28.0 AGROW GEN3 ST6 2.8E-6 3.5E-5 4.0 4.0 UP HWANG VECTAU U10PROXY 32.0 AGROW GEN3 ST6 2.8E-6 3.5E-5 4.0 4.0 UP HWANG VECTAU U10PROXY 32.0 DEBIAS 0.89 AGROW GEN3 ST6 6.5E-6 8.5E-5 4.0 4.0 UP HWANG VECTAU U10PROXY 35.0 AGROWNote the different values of coefficients [a1sds] and [a2sds] in case of different U10PROXY settings! Usually one of the following two lines is recommended in regular SWAN simulations. Here, the command SSWELL for swell dissipation must be indicated using a separate line (see below).
GEN3 ST6 4.7E-7 6.6E-6 U10P 28. AGROW GEN3 ST6 2.8E-6 3.5E-5 U10P 32. AGROWFinally, the following two lines represent the original model described by RBW12 (see their Table 1, page 1336). Also SSWELL must be indicated using a separate line (see below).
GEN3 ST6 5.7E-7 8.0E-6 4.0 4.0 UP HWANG U10PROXY 28.0 AGROW GEN3 ST6 5.7E-7 8.0E-6 4.0 4.0 UP AGROW
| JANSSEN | linear growth | : Cavaleri and Malanotte-Rizzoli (1981), activated only |
| if the keyword AGROW is present (see below) | ||
| exponential growth | : Janssen (1989, 1991). | |
| [cds1] | coefficient for determining the rate of whitecapping dissipation (=
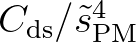 ). ). |
|
| Default: [cds1] = 4.5. | ||
| [delta] | coefficient which determines the dependency of the whitecapping on wave number | |
| (mix with Komen et al. formulation). | ||
| Default: [delta] = 0.5. | ||
| KOMEN | linear growth | : Cavaleri and Malanotte-Rizzoli (1981), activated only |
| if the keyword AGROW is present (see below) | ||
| exponential growth | : Komen et al. (1984). | |
| [cds2] | coefficient for determining the rate of whitecapping dissipation (=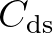 ). ). |
|
| Default: [cds2] = 2.36e-5. | ||
| [stpm] | value of the wave steepness for a Pierson-Moskowitz spectrum (=
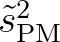 ). ). |
|
| Default: [stpm] = 3.02e-3. | ||
| WESTH | nonlinear saturation-based whitecapping combined with wind input of Yan (1987). | |
| This option is the default. | ||
| DRAG | indicates the wind drag formulation. | |
| WU | wind drag formula according to Wu (1982). | |
| This option is the default. | ||
| FIT | drag coefficient is based on second order polynomial fit (see Zijlema et al., 2012). | |
| ST6 | wind input and whitecapping from Rogers et al. (2012). | |
| [a1sds] | coefficient related to local dissipation term 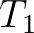 . . |
|
| [a2sds] | coefficient related to cumulative dissipation term 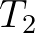 . . |
|
| [p1sds] | power coefficient controlling strength of dissipation term 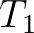 . . |
|
| Default: [p1sds] = 4. | ||
| [p2sds] | power coefficient controlling strength of dissipation term 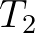 . . |
|
| Default: [p2sds] = 4. | ||
| UP | select 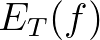 for normalization of exceedance level. for normalization of exceedance level. |
|
| This option is the default. | ||
| DOWN | select 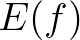 for normalization of exceedance level. for normalization of exceedance level. |
|
| HWANG | wind drag formula according to Hwang (2011). | |
| This option is the default. | ||
| Note: the drag formula of Zijlema et al (2012) will not be applied! | ||
| FAN | wind drag formula according to Fan et al. (2012). | |
| ECMWF | wind drag formula based on WAM Cycle 4 (Janssen). | |
| VECTAU | use vector integral for computing wind stress. | |
| This option is the default. | ||
| SCATAU | use scalar integral for computing wind stress. | |
| TRUE10 | wind velocity based on 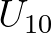 . . |
|
| U10PROXY | 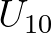 = [windscaling] = [windscaling]
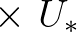 . . |
|
| This option is the default. | ||
| [windscalin] | factor to scale 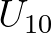 with with 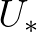 . . |
|
| Default: [windscaling] = 28. | ||
| DEBIAS | allows user to counter bias in the input wind field. | |
| [cdfac] | multiplier on drag coefficient. | |
| Default: [cdfac] = 1. | ||
| AGROW | if this keyword is used, the wave growth term of Cavaleri and Malanotte (1981) is | |
| activated. | ||
| if this keyword is NOT used, the wave growth term of Cavaleri and Malanotte (1981) | ||
| is NOT activated. | ||
| Note that in nonstationary runs SWAN start with INIT ZERO (see command INIT), | ||
| wave energy remains zero unless wave energy penetrates over the boundary or AGROW | ||
| is activated. In case of stationary runs, however, SWAN will start with a first guess. | ||
| [a] | if the wave growth term of Cavaleri and Malanotte (1981) is activated, [a] is | |
| the proportionality coefficient in that term. | ||
| Default: [a] = 0.0015. |
| -> ARDhuin [cdsv]
SSWELL <
| ZIEger [b1]

With this command the user can influence the type of swell dissipation included in the computations.
The Zieger option is intended for use with negative wind input via the NEGATINP command.
Zieger non-breaking dissipation follows the method used in WAVEWATCH III version 4 and does not
include the steepness-dependent swell coefficient introduced in WAVEWATCH III version 5.
As noted already, if GEN3 ST6... command is used, this SSWELL command should be provided.
Examples:
SSWELL ARDHUIN 1.2 SSWELL ZIEGER 0.00025 NEGATINP 0.04
| ARDHUIN | non-breaking dissipation of Ardhuin et al. (2010). | |
| [cdsv] | coefficient related to laminar atmospheric boundary layer. | |
| Default: [cdsv] = 1.2 | ||
| ZIEGER | non-breaking dissipation of Young et al. (2013), updated by Zieger et al. (2015). | |
| [b1] | non-dimensional proportionality coefficient. |
NEGatinp [rdcoef]

With this optional command the user activates negative wind input.
This is intended only for use with non-breaking swell dissipation SSWELL ZIEGER.
Parameter [rdcoef] is a fraction between 0 and 1, representing the strength of negative wind input.
As an example, with [rdcoef]=0.04, for a spectral bin that is opposed to the wind direction,
the wind input factor 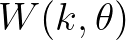 is negative,
and its magnitude is 4% of the corresponding value of the spectral bin that is in the opposite direction (i.e. in the wind direction).
See Zieger et al. (2015) eq. 11, where
is negative,
and its magnitude is 4% of the corresponding value of the spectral bin that is in the opposite direction (i.e. in the wind direction).
See Zieger et al. (2015) eq. 11, where 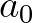 is their notation for [rdcoef].
Default [rdcoef]=0.0 and [rdcoef]=0.04 is recommended, though as implied by Zieger et al. (2015),
this value is not well-established, so the user is encouraged to experiment with other values.
is their notation for [rdcoef].
Default [rdcoef]=0.0 and [rdcoef]=0.04 is recommended, though as implied by Zieger et al. (2015),
this value is not well-established, so the user is encouraged to experiment with other values.
| KOMen [cds2] [stpm] [powst] [delta] [powk]
WCAPping <
| -> AB [cds2] [br] CURrent [cds3]

With this command the user can influence whitecapping which is usually included in the computations. Can be de-activated with command OFF WCAP.
| KOMEN | whitecapping according to Komen et al. (1984) is applied. | |
| [cds2] | coefficient for determining the rate of whitecapping dissipation (=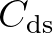 ). ). |
|
| Default: [cds2] = 2.36e-5. | ||
| [stpm] | value of the wave steepness for a Pierson-Moskowitz spectrum (=
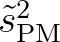 ). ). |
|
| Default: [stpm] = 3.02e-3. | ||
| [powst] | power of steepness normalized with the wave steepness of a Pierson-Moskowitz | |
| spectrum. | ||
| Default: [powst] = 2. | ||
| [delta] | coefficient which determines the dependency of the whitecapping on wave number. | |
| Default: [delta] = 1. | ||
| Note that this default has been changed since version 40.91A. The setting | ||
| [delta] = 1 will improve the prediction of the wave energy at low frequencies, | ||
| and hence the mean wave period. The original default was [delta] = 0, which | ||
| corresponds to WAM Cycle 3. See the Scientific/Technical documentation for | ||
| further details. | ||
| [powk] | power of wave number normalized with the mean wave number. | |
| Default: [powk] = 1. | ||
| AB | whitecapping according to Alves and Banner (2003) is applied. | |
| See also the paper of Van der Westhuysen et al. (2007). | ||
| This is the default. | ||
| [cds2] | proportionality coefficient due to Alves and Banner (2003). | |
| Default: [cds2] = 5.0e-5. | ||
| [br] | threshold saturation level. | |
| Default: [br] = 1.75e-3. | ||
| CURRENT | indicates that enhanced current-induced dissipation as proposed by | |
| Van der Westhuysen (2012) is to be added. | ||
| [cds3] | proportionality coefficient. | |
| Default: [cds3] = 0.8. |
QUADrupl [iquad] [lambda] [Cnl4] [Csh1] [Csh2] [Csh3]

With this option the user can influence the computation of nonlinear quadruplet wave interactions which are usually included
in the computations. Can be de-activated with command OFF QUAD.
Note that the DIA approximation of the quadruplet interactions
is a poor approximation for long-crested waves and frequency resolutions that are deviating much more than 10% (see command CGRID).
Note that DIA is usually updated per sweep, either semi-implicit ([iquad] = 1) or explicit ([iquad] = 2).
However, when ambient current is included, the bounds of the directional sector within a sweep may be different for each frequency bin
(particularly the higher frequencies are modified by the current). So there may be some overlap of frequency bins between the sweeps,
implying non-conservation of wave energy. To prevent this the user is advised to choose the integration of DIA per iteration instead of per sweep,
i.e. [iquad] = 3.
If you want to speed up your computation a bit more, than the choice [iquad] = 8 is a good choice.
| [iquad] | the quadruplets can be integrated by four different numerical procedures: | |
| = 1 semi-implicit computation of the nonlinear transfer with DIA per sweep | ||
| = 2 fully explicit computation of the nonlinear transfer with DIA per sweep | ||
| = 3 fully explicit computation of the nonlinear transfer with DIA per iteration | ||
| = 8 fully explicit computation of the nonlinear transfer with DIA per iteration, | ||
| but neighbouring interactions are interpolated in piecewise constant manner. | ||
| other techniques for the computation of quadruplets are | ||
| = 4 Multiple DIA | ||
| = 51 XNL (deep water transfer) | ||
| = 52 XNL (deep water transfer with WAM depth scaling) | ||
| = 53 XNL (finite depth transfer) | ||
| Default: [iquad] = 2. | ||
| [lambda] | coefficient for quadruplet configuration in case of DIA. | |
| Default: [lambda]=0.25. | ||
| [Cnl4] | proportionality coefficient for quadruplet interactions in case of DIA. | |
Default: [Cnl4]=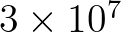 . . |
||
| [Csh1] | coefficient for shallow water scaling in case of DIA. | |
| Default: [Csh1]=5.5. | ||
| [Csh2] | coefficient for shallow water scaling in case of DIA. | |
| Default: [Csh2]=0.833333. | ||
| [Csh3] | coefficient for shallow water scaling in case of DIA. | |
Default: [Csh3]= 1.25. 1.25. |
| -> CONstant [alpha] [gamma]
BREaking <
| BKD [alpha] [gamma0] [a1] [a2] [a3]

With this command the user can influence depth-induced wave breaking in shallow water.
If this command is not used, SWAN will account for wave breaking anyhow (with default options and
values). If the user wants to specifically ignore wave breaking, he should use the command: OFF BREAKING.
| CONSTANT | indicates that a constant breaker index is to be used. | |
| [alpha] | proportionality coefficient of the rate of dissipation. | |
| Default: [alpha] = 1.0. | ||
| [gamma] | the breaker index, i.e. the ratio of maximum individual | |
| wave height over depth. | ||
| Default: [gamma] = 0.73. | ||
| BKD | indicates that the breaker index scales with both the | |
bottom slope (=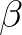 ) and the dimensionless depth (= ) and the dimensionless depth (=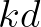 ) ) |
||
| [alpha] | proportionality coefficient of the rate of dissipation. | |
| Default: [alpha] = 1.0. | ||
| [gamma0] | the reference 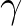 for horizontal slopes. for horizontal slopes. |
|
| Default: [gamma0] = 0.54. | ||
| [a1] | first tunable coefficient for the breaker index. | |
| Default: [a1] = 7.59. | ||
| [a2] | second tunable coefficient for the breaker index. | |
| Default: [a2] = -8.06. | ||
| [a3] | third tunable coefficient for the breaker index. | |
| Default: [a3] = 8.09. |
| -> JONswap CONstant [cfjon]
|
| COLLins [cfw]
FRICtion <
| MADsen [kn]
|
| RIPples [S] [D]

With this optional command the user can activate bottom friction. If this command is not used, SWAN will not account for bottom friction.
In SWAN four different formulations are available, i.e., that of Hasselmann et al. (1973, JONSWAP),
Collins (1972), Madsen et al. (1988) and Smith et al. (2011).
The default option is: JONSWAP with a constant friction coefficient. The recommended value for typical sandy bottoms is
0.038 m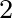 s
s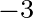 . Note that this value is to be applied for both wind sea and swell conditions.
(The use of the previous default value of 0.067 m
. Note that this value is to be applied for both wind sea and swell conditions.
(The use of the previous default value of 0.067 m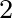 s
s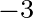 is discouraged, even for wind sea conditions!)
For smoother seafloors, like the Gulf of Mexico, a lower value of 0.019 m
is discouraged, even for wind sea conditions!)
For smoother seafloors, like the Gulf of Mexico, a lower value of 0.019 m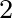 s
s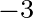 is advised.
is advised.
| JONSWAP | indicates that the semi-empirical expression derived from the JONSWAP results | |
| for bottom friction dissipation (Hasselmann et al., 1973, JONSWAP) should be | ||
| activated. This option is the default. | ||
| CONSTANT | this default option indicates that the JONSWAP coefficient is constant. | |
| [cfjon] | coefficient of the JONSWAP formulation. | |
| Default: [cfjon] = 0.038. | ||
| COLLINS | indicates that the expression of Collins (1972) should be activated. | |
| [cfw] | Collins bottom friction coefficient. | |
| Default: [cfw] = 0.015. | ||
| Note that [cfw] is allowed to vary over the computational region; in that | ||
| case use the commands INPGRID FRICTION and READINP FRICTION to define | ||
| and read the friction data. The command FRICTION is still required to define | ||
| the type of friction expression. The value of [cfw] in this command is then | ||
| not required (it will be ignored). | ||
| MADSEN | indicates that the expression of Madsen et al. (1988) should be activated. | |
| [kn] | equivalent roughness length scale of the bottom (in m). | |
| Default: [kn] = 0.05. | ||
| Note that [kn] is allowed to vary over the computational region; in that case | ||
| use the commands INPGRID FRICTION and READINP FRICTION to define and read | ||
| the friction data. This command FRICTION is still required to define the type of | ||
| friction expression. The value of [kn] in this command is then not required | ||
| (it will be ignored). | ||
| RIPPLES | indicates that the expression of Smith et al. (2011) should be activated. | |
| Here friction depends on the formation of bottom ripples and sediment size. | ||
| [S] | the specific gravity of the sediment. | |
| Default: [S] = 2.65. | ||
| [D] | the sediment diameter (in m). | |
| Default: [D] = 0.0001. |
| / -> COLL |
| -> DCTA [trfac] [p] \ NONC |
| |
| LTA [trfac] |
TRIad < > &
| FTIM [trfac] |
| |
| SPB [trfac] [a] |
| -> ELDeberky [urcrit] | | FG
BIPHase < > TRAnsfer < MS
| DEWIT [lpar] | | BRedmose
| -> QUadwave

With this command the user can activate the triad wave-wave interactions.
If this command is not used, SWAN will not account for triads.
| DCTA | indicates that the DCTA method of Booij et al. (2009) should be activated. | |
| This option is the default. | ||
| [trfac] | scaling factor that controls the intensity of the triad interaction due to DCTA. | |
| Default: [trfac] = 4.4. | ||
| [p] | shape coefficient to force the high-frequency tail. | |
| Default: [p] = 4/3. | ||
| COLL | indicates that the triad interactions due to DCTA are restricted to collinear ones | |
| only. This is the default. | ||
| NONC | indicates to include noncollinear interactions within the DCTA framework. | |
| LTA | indicates that the extended LTA method should be activated. | |
| [trfac] | scaling factor that controls the intensity of the triad interaction due to LTA. | |
| Default: [trfac] = 1.0. | ||
| FTIM | indicates that the full triad interaction model (FTIM) should be activated. | |
| [trfac] | scaling factor that controls the intensity of the triad interaction due to FTIM. | |
| Default: [trfac] = 1.0. | ||
| SPB | indicates that the SPB method of Becq-Girard et al. (1999) should be activated. | |
| [trfac] | scaling factor that controls the intensity of the triad interaction due to SPB. | |
| Default: [trfac] = 0.9. | ||
| [a] | calibration parameter for tuning 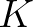 in Eq. (5.1) of Becq-Girard et al. (1999). in Eq. (5.1) of Becq-Girard et al. (1999). |
|
| This parameter is associated with relaxation of the resonance condition and | ||
is a function of the local wave number:
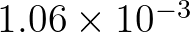 . . |
||
| Note that with the current tuning the nonlinear interaction coefficient of | ||
| Madsen and Sørensen (1993) will be employed, unless specified otherwise | ||
| (see the keyword TRANSFER below). | ||
| Default: [a] = 0.95. | ||
| BIPHASE | defines the parametrization of biphase. | |
| Note: this option does not applied to the SPB method. | ||
| ELDEBERKY | the biphase parametrization as function of Ursell number as given by | |
| Eldeberky (1996) will be used. This is the default. | ||
| [urcrit] | the critical Ursell number appearing in the parametrization. | |
| Note: the value of [urcrit] is setted by Eldeberky (1996) at 0.2 based on a | ||
| laboratory experiment, whereas Doering and Bowen (1995) employed the value | ||
| of 0.63 based on the field experiment data. | ||
| Default: [urcrit] = 0.63. | ||
| DEWIT | De Wit (2022) proposed a parametrization of the biphase evolution based on | |
| the local bed slope and peak wave period. | ||
| [lpar] | scales spatial averaging of the De Wit's biphase in terms of a multiple of peak | |
| wave length of the incident wave field. | ||
| Note: [lpar] = 0 means no averaging. | ||
| Default: [lpar] = 0. | ||
| TRANSFER | defines the interaction coefficient to describe the nonlinear energy transfers | |
| in triads of shoaling waves. | ||
| Note: this option does not applied to the DCTA method. | ||
| FG | Freilich and Guza (1984) suggested the use of the Boussinesq-wave model | |
| of Peregrine (1967) to compute the interaction coefficient. | ||
| MS | the nonlinear transfer coefficient derived from the Boussinesq-wave theory | |
| of Madsen and Sørensen (1993) is employed. | ||
| BREDMOSE | The exact transfer coefficient (second order Stokes solution) of | |
| Bredmose et al (2005) is applied. | ||
| QUADWAVE | Akrish et al (2024) proposed the parametrized transfer coefficient that | |
| optimizes the nonlinearity of the fully dispersive quadratic wave model | ||
| of Bredmose et al (2005). | ||
| This is the default. |
VEGEtation [iveg] < [height] [diamtr] [nstems] [drag] >

With this command the user can activate wave damping due to vegetation based on the Dalrymple's formula (1984) as implemented by Suzuki et al. (2011).
This damping is uniform over the wave frequencies. An alternative is the frequency-dependent (canopy) dissipation model of Jacobsen et al. (2019).
If this command is not used, SWAN will not account for vegetation effects.
The vegetation (rigid plants) can be divided over a number of vertical segments and so, the
possibility to vary the vegetation vertically is included. Each vertical layer represents some characteristics of the plants. These
variables as indicated below can be repeated as many vertical layers to be chosen.
Note that with respect to the Jacobsen et al. (2019) method, vertical layering of the vegetation is not yet implemented.
| [iveg] | indicates the method for the vegetation computation: | |
| = 1 Suzuki et al. (2011) | ||
| = 2 Jacobsen et al. (2019) | ||
| Default: [iveg] = 1. | ||
| [height] | the plant height per layer (in m). | |
| [diamtr] | the diameter of each plant stand per layer (in m). | |
| [nstems] | the number of plant stands per square meter for each layer. | |
| Note that [nstems] is allowed to vary over the computational region to | ||
| account for the zonation of vegetation. In that case use the commands | ||
| INPGRID NPLANTS and READINP NPLANTS to define and read the vegetation | ||
| density. The (vertically varying) value of [nstems] in this command will | ||
| be multiplied by this horizontally varying plant density. | ||
| Default: [nstems] = 1. | ||
| [drag] | the drag coefficient per layer. |
MUD [layer] [rhom] [viscm]

With this command the user can activate wave damping due to mud based on Ng (2000). If this command or the commands
INPGRID MUDLAY and READINP MUDLAY are not used, SWAN will not account for muddy bottom effects.
| [layer] | the thickness of the mud layer (in m). | |
| Note that [layer] is allowed to vary over the computational region to | ||
| account for the zonation of muddy bottom. In that case use the commands | ||
| INPGRID MUDLAY and READINP MUDLAY to define and read the layer | ||
| thickness of mud. The value of [layer] in this command is then not | ||
| required (it will be ignored). | ||
| [rhom] | the density of the mud layer (in kg/m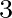 ). ). |
|
| Default: [rhom] = 1300. | ||
| [viscm] | the kinematic viscosity of the mud layer (in m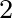 /s). /s). |
|
| Default: [viscm] = 0.0076. |
| -> R19 [c0] [c1] [c2] [c3] [c4] [c5] [c6]
SICE < D15 [Chf]
| M18 [Chf]
| R21B [Chf npf]

Using this command, the user activates a sink term to represent the dissipation of wave energy by sea ice. The R19 method is empirical/parametric: a polynomial based on wave frequency
(Rogers, 2019). This polynomial (in 1/m) has seven dimensional coefficients; see Scientific/Technical documentation for details.
If this command is not used, SWAN will not account for sea ice effects.
Note that it is also necessary to describe the ice, using the ICE command (for uniform and stationary ice) or INPgrid/READinp commands (for variable ice).
The default R19 setting is the case of c2=
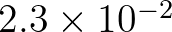 and c4=
and c4=
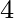 . Thus, the following commands are equivalent
. Thus, the following commands are equivalent
| [aice] | ice concentration as a fraction from 0 to 1. | |
| Note that [aice] is allowed to vary over the computational region to account | ||
| for the zonation of ice concentration. In that case use the commands | ||
| INPGRID AICE and READINP AICE to define and read the sea concentration. | ||
| The value of [aice] in this command is then not required (it will be | ||
| ignored). | ||
| [c0] | polynomial coefficient (in 1/m) for determining the rate of sea ice dissipation. | |
| [c1] | polynomial coefficient (in s/m) for determining the rate of sea ice dissipation. | |
| [c2] | polynomial coefficient (in s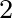 /m) for determining the rate of sea ice dissipation. /m) for determining the rate of sea ice dissipation. |
|
| [c3] | polynomial coefficient (in s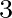 /m) for determining the rate of sea ice dissipation. /m) for determining the rate of sea ice dissipation. |
|
| [c4] | polynomial coefficient (in s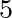 /m) for determining the rate of sea ice dissipation. /m) for determining the rate of sea ice dissipation. |
|
| [c5] | polynomial coefficient (in s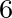 /m) for determining the rate of sea ice dissipation. /m) for determining the rate of sea ice dissipation. |
|
| [c6] | polynomial coefficient (in s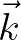 /m) for determining the rate of sea ice dissipation. /m) for determining the rate of sea ice dissipation. |
|
| [Chf] | a simple coefficient of proportionality. | |
| [npf] | controls the degree of dependence on frequency and ice thickness. |
TURBulence [ctb] (CURrent [tbcur])

With this optional command the user can activate turbulent viscosity.
This physical effect is also activated by reading values of the turbulent viscosity
using the READGRID TURB command, but then with the default value of [ctb].
The command READGRID TURB is necessary if this command TURB is used since the
value of the viscosity is assumed to vary over space.
| [ctb] | the value of the proportionality coefficient appearing in the energy | |
| dissipation term. | ||
| Default: [ctb] = 0.01. | ||
| CURRENT | if this keyword is present the turbulent viscosity will be derived from the | |
| product of the depth and the absolute value of the current velocity. If the | ||
| command READGRID TURB is used, this option is ignored; the values read | ||
| from file will prevail. | ||
| [tbcur] | the factor by which depth  current velocity is multiplied in order to current velocity is multiplied in order to |
|
| get the turbulent viscosity. | ||
| Default: [tbcur] = 0.004. |
BRAGg [ibrag] [nreg] [cutoff] &
| -> FT
<
| FILE 'fname' [idla] [mkx] [mky] [dkx] [dky]

Using this optional command, the user activates a source term to represent the scattering of waves due to
changes in the small-scale bathymetry based on the theory of Ardhuin and Herbers (2002).
If this command is not used, SWAN will not account for Bragg scattering.
The underlying process is related to the bed elevation spectrum that
describes the random variability of the bathymetry at the scale of the wave length on top of a slowly varying depth. To input this spectrum in the model, two options
are available. One option is to read a spectrum from a file. This single bottom spectrum will subsequently be applied in all active grid points.
The assumption being made here is that the inputted bottom is gently sloping. Note that the bottom spectrum must be given as a function of the wave number 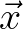 .
.
Another option is to compute the spectrum by a Fourier transform from 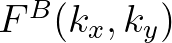 to
to 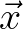 of the bed modulations around a computational grid point.
First, one must define a square region with a fixed size around the grid point in order to perform the Fourier transform. The size should correspond to a multiple of the
wave length at which refraction is resolved (i.e. consistent with the mild slope assumption). Next, the amplitude modulation of the small-scale bathymetry
is obtained by substracting a slowly varying bed level from the inputted high-resolution bathymetric data within this square region. Here, the smooth bed level is achieved
using a bilinear fit. During the computation, however, SWAN employs the gently sloping bed as the mean of the original bathymetry within the given square around each
computational grid point. Finally, the corresponding bottom spectrum is computed with an FFT.
of the bed modulations around a computational grid point.
First, one must define a square region with a fixed size around the grid point in order to perform the Fourier transform. The size should correspond to a multiple of the
wave length at which refraction is resolved (i.e. consistent with the mild slope assumption). Next, the amplitude modulation of the small-scale bathymetry
is obtained by substracting a slowly varying bed level from the inputted high-resolution bathymetric data within this square region. Here, the smooth bed level is achieved
using a bilinear fit. During the computation, however, SWAN employs the gently sloping bed as the mean of the original bathymetry within the given square around each
computational grid point. Finally, the corresponding bottom spectrum is computed with an FFT.
An important note to be made here is the fact that adding the Bragg scattering source term to the action balance equation gives rise to a fairly stiff equation.
The best remedy is to run SWAN in the nonstationary mode with a relatively small time step or in the stationary mode with some under relaxation
(see command NUM STAT [alfa]).
| [ibrag] | indicates the computation of Bragg scattering term: | |
| = 1 source term is calculated per sweep and bottom spectrum is | ||
| interpolated at the difference wave number a priori (thus | ||
| requiring storage) | ||
| = 2 source term is calculated per sweep and bottom spectrum is | ||
| interpolated at the difference wave number per sweep (no storage) | ||
| = 3 source term is calculated per iteration and bottom spectrum is | ||
| interpolated at the difference wave number per iteration (no storage) | ||
| Default: [ibrag] = 1. | ||
| [nreg] | size of square region around computational grid point (centered) for computing | |
| the mean depth and, if desired, the bed elevation spectrum. It is expressed in | ||
| terms of the number of grid points (per direction) of the inputted bottom grid. | ||
| [cutoff] | cutoff to the ratio between surface and bottom wave numbers. | |
| Note: see the Scientific/Technical documentation for details. | ||
| Default: [cutoff] = 5. | ||
| FT | if this keyword is present the bottom spectrum will be computed in each active | |
| grid point using an FFT. | ||
| Note: the depth in each computational grid point is computed as the average of | ||
| the inputted (high-resolution) bed levels within the square region. | ||
| FILE | means that the bed elevation spectrum
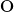 is read from a file. is read from a file. |
|
| Note: this spectrum is taken to be uniform over the entire computational domain. | ||
| 'fname' | name of the file containing the bottom spectrum. | |
| [idla] | prescribes the order in which the spectra values should be given in the file; | |
| see command READINP. | ||
| [mkx] | number of cells in 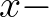 direction of the wave number grid related to bottom spectrum direction of the wave number grid related to bottom spectrum |
|
| (this number is one less than the number of points in this direction!) | ||
| [mky] | number of cells in 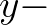 direction of the wave number grid related to bottom spectrum direction of the wave number grid related to bottom spectrum |
|
| (this number is one less than the number of points in this direction!) | ||
| Default: [mky] = [mkx]. | ||
| [dkx] | mesh size in 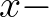 direction of the wave number grid related to bottom spectrum (1/m). direction of the wave number grid related to bottom spectrum (1/m). |
|
| [dky] | mesh size in  direction of the wave number grid related to bottom spectrum (1/m). direction of the wave number grid related to bottom spectrum (1/m). |
|
| Default: [dky] = [dkx]. |
LIMiter [ursell] [qb]

With this command the user can de-activate permanently the quadruplets when the actual Ursell number
exceeds [ursell]. Moreover, as soon as the actual fraction of breaking waves exceeds [qb] then the action limiter
will not be used in case of decreasing action density.
| [ursell] | the upper threshold for Ursell number. | |
| Default: [ursell] = 10.0. | ||
| [qb] | the threshold for fraction of breaking waves. | |
| Default: [qb] = 1.0. |
| -> TRANSm [trcoef] |
| |
| TRANS1D < [trcoef] > |
| |
OBSTacle < TRANS2D < [trcoef] > > &
| |
| | -> GODA [hgt] [alpha] [beta] |
| DAM < |
| DANGremond [hgt] [slope] [Bk] |
| -> RSPEC |
( REFL [reflc] < > ) &
| RDIFF [pown] |
( FREEboard [hgt] [gammat] [gammar] Quay ) LINe <[xp] [yp]>

CANNOT BE USED IN 1D-MODE.
With this optional command the user provides the characteristics of a (line of) sub-grid obstacle(s)
through which waves are transmitted or against which waves are reflected (possibly both at the same
time). The obstacle is sub-grid in the sense that it is narrow
compared to the spatial meshes; its length should be at least one mesh length.
The location of the obstacle is defined by a sequence of corner points of a line. The obstacles interrupt
the propagation of the waves from one grid point to the next wherever this obstacle line is located between
two neighbouring grid points (of the computational grid; the resolution of the obstacle is therefore equal
to the computational grid spacing). This implies that an obstacle to be effective must be located such that
it crosses at least one grid line. This is always the case when an obstacle is larger than one mesh
length.
The computation of transmission and reflection is problematic if an obstacle runs exactly through one or
more grid points of the computational structured grid; SWAN will move the obstacle over a small
distance (1% of the mesh size) if this occurs. Note that this will not be done in case of unstructured
grids.
The reflection results are incorrect if more than one obstacle crosses the
same grid line between two neighbouring grid points. SWAN is not able to detect this, so the user must
check if his model fulfills this condition.
| TRANSM | with this option the user indicates that the transmission coefficient is a constant. | |
| [trcoef] | constant transmission coefficient, formulated in terms of wave height, i.e. ratio | |
| of transmitted significant wave height over incoming significant wave height. | ||
| Default: [trcoef]=0.0 (no transmission = complete blockage). | ||
| TRANS1D | with this option the user indicates that the transmission coefficient is frequency | |
| dependent. For each frequency the user can specify a transmission coefficient as | ||
| indicated below. The number of these transmission values must be equal to the | ||
| number of frequencies, i.e. [msc] + 1. | ||
| [trcoef] | transmission coefficient per frequency, formulated in terms of wave height, i.e. | |
| ratio of transmitted significant wave height over incoming significant wave height. | ||
| TRANS2D | with this option the user indicates that the transmission coefficient is frequency | |
| and direction dependent. For each direction the user can assign different trans- | ||
| mission coefficients to frequencies. The number of these transmission values must | ||
| be equal to the number of frequencies multiplied by the number of directions. | ||
| [trcoef] | transmission coefficient per frequency for each direction, formulated in terms of | |
| wave height, i.e. ratio of transmitted significant wave height over incoming | ||
| significant wave height. It is advised to put the values assigned to all frequencies | ||
| on a single line for each direction. So the number of lines equals the number of | ||
| directions. Each line may be terminated with a continuation mark &. | ||
| DAM | with this option the user indicates that the transmission coefficient depends on | |
| the incident wave conditions at the obstacle and on the obstacle height (which | ||
| may be submerged). | ||
| GODA | with this option the user indicates to use the Goda/Seelig formula (1979) for | |
| computing transmission coefficient. | ||
| [hgt] | the elevation of the top of the obstacle above reference level (same reference | |
| level as for bottom etc.); use a negative value if the top is below that reference | ||
| level. If this command is used, this value is required. | ||
| [alpha] | coefficient determining the transmission coefficient for Goda's transmission formula. | |
| Default: [alpha]=2.6. | ||
| [beta] | another coefficient determining the transmission coefficient for Goda's transmission | |
| formula. | ||
| Default: [beta]=0.15. | ||
| DANGREMOND | with this option the user indicates to use the d'Angremond/Van der Meer formula | |
| (1996) for computing the transmission coefficient. | ||
| [hgt] | the elevation of the top of the obstacle above reference level (same reference | |
| level as for bottom etc.); use a negative value if the top is below that reference | ||
| level. If this command is used, this value is required. | ||
| [slope] | the slope of the obstacle (in degrees). If this command is used, this value is required. | |
| [Bk] | the crest width of the obstacle. If this command is used, this value is required. | |
| REFL | if this keyword is present the obstacle will reflect wave energy (possibly in | |
| combination with transmission). Reflections will be computed only if the spectral | ||
directions cover the full 360 , i.e. if in the command CGRID the option CIRCLE , i.e. if in the command CGRID the option CIRCLE |
||
| is activated. | ||
| [reflc] | constant reflection coefficient, formulated in terms of wave height, i.e. ratio | |
| of reflected significant wave height over incoming significant wave height. | ||
Restriction: 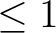 [reflc] [reflc] 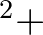 . . |
||
| Default: [reflc]=1, if the keyword REFL is present, otherwise [reflc]=0. | ||
Note: the program checks if the criterion [reflc]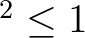 [trcoef] [trcoef] is is |
||
| fulfilled. | ||
| RSPEC | indicates specular reflection which is the default. The angle of reflection | |
| equals the angle of incidence. | ||
| RDIFF | indicates diffuse reflection, i.e. specular reflection where incident waves | |
| are scattered over reflected direction. | ||
| [pown] | each incoming direction  is scattered over reflected direction is scattered over reflected direction
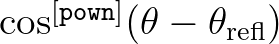 |
|
according to
![$\cos^{{\tt [pown]}} (\theta - \theta_{\rm refl})$](img108.png) . The parameter [pown] indicates the width . The parameter [pown] indicates the width |
||
| of the redistribution function. | ||
| Default: [pown] = 1. | ||
| FREEBOARD | with this option the user indicates that the fixed transmission [trcoef] | |
| and reflection [reflc] coefficients are freeboard dependent. The freeboard | ||
| dependency has no effect on the transmission coefficient as computed using | ||
| the DAM option. | ||
| [hgt] | the elevation of the top of the obstacle or height of the quay above the reference | |
| level (same reference level as for the bottom). Use a negative value if the top is | ||
| below that reference level. Specifying this parameter is required when option | ||
| FREE is used. In case [hgt] is also specified in the DAM option, both values of | ||
| [hgt] should be equal for consistency. | ||
| [gammat] | shape parameter of relative freeboard dependency of transmission coefficient. | |
| This parameter should be higher than zero. See Scientific/Technical documentation | ||
| for background information. | ||
| Default: [gammat] = 1. | ||
| [gammar] | shape parameter of relative freeboard dependency of reflection coefficient. | |
| This parameter should be higher than zero. See Scientific/Technical documentation | ||
| for background information. | ||
| Default: [gammar] = 1. | ||
| QUAY | with this option the user indicates that the freeboard dependency of the transmission | |
| and reflection coefficients also depends on the relative position of an obstacle-linked | ||
| grid point with respect to the position of the obstacle line representing the edge of a | ||
| quay. In case the active grid point is on the deeper side of the obstacle, then the | ||
| correction factors are applied using the parameters [hgt], [gammat] and [gammar]. | ||
| In case the active grid point is on the shallower side of the obstacle, the reflection | ||
| coefficient is set to 0 and the transmission coefficient to 1. This option only works | ||
| in combination with the keyword FREE. See Scientific/Technical documentation | ||
| for background information. | ||
| LINE | with this required keyword the user defines the location of the obstacle(s). | |
| [xp], [yp] | coordinates of a corner point of the line that defines the location of the | |
| obstacle(s) (in problem coordinates): | ||
| if Cartesian coordinates are used in m or | ||
| if spherical coordinates are used in degrees (see command COORD). | ||
| At least two corner points must be provided. |
OBSTacle FIG [alpha1] [hss] [tss] [dss] [dd] REFL [reflc] LINe <[xp] [yp]>

CANNOT BE USED IN 1D-MODE.
With this optional command the user specifies the obstacles along which the free infragravity (FIG)
energy is radiated. By placing the obstacles close to the shorelines SWAN will include the FIG
source term along the coastlines according to the parametrization of Ardhuin et al. (2014).
The location of the obstacle is defined by a sequence of corner points of a line.
For an obstacle line to be effective its length is at least one mesh size large.
It is recommended to place the obstacles at the inner area of the computational grid, not at or
through the boundaries. In particular, each obstacle line must be bordered by wet points on
both sides.
In addition, the orientation of the obstacle line determines from which side of the obstacle
the FIG wave energy is radiated away. If the begin point of the line is below or left of the end point,
that is, pointing upwards/to the right, then FIG energy is radiated from the west/north side of the line.
If the begin point is above or right of the end point (pointing downwards/to the left), then FIG energy
is radiated away from the east/south side of the obstacle line.
| FIG | with this option the user indicates that FIG source term is included along | |
| the obstacle(s). It will be included only if the spectral directions cover the | ||
full 360 , i.e. if in the command CGRID the option CIRCLE is activated. , i.e. if in the command CGRID the option CIRCLE is activated. |
||
| [alpha1] | calibration parameter (in 1/s) for determining the rate of radiating FIG | |
| energy from the shorelines. | ||
| [hss] | the sea-swell significant wave height (in m). | |
| [tss] | a sea-swell mean wave period (in s). | |
| [dss] | the sea-swell mean wave direction (in degrees). | |
| Default: [dss]=-999. | ||
| [dd] | power 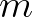 of directional spreading of directional spreading 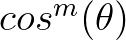 for radiated FIG. for radiated FIG. |
|
| Default: [dd]=0. | ||
| REFL | if this keyword is present then any shoreward propagating (FIG) wave is | |
| specular reflected. | ||
| [reflc] | constant reflection coefficient, formulated in terms of wave height, i.e. ratio | |
| of reflected significant wave height over incoming significant wave height. | ||
Restriction: 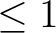 [reflc] [reflc] 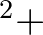 . . |
||
| Default: [reflc]=1, if the keyword REFL is present, otherwise [reflc]=0. | ||
| LINE | with this required keyword the user defines the location of the obstacle(s). | |
| [xp], [yp] | coordinates of a corner point of the line that defines the location of the | |
| obstacle(s) (in problem coordinates): | ||
| if Cartesian coordinates are used, in m, or | ||
| if spherical coordinates are used, in degrees (see command COORD). | ||
| At least two corner points must be provided. |
SETUP [supcor]

CANNOT BE USED IN CASE OF UNSTRUCTURED GRIDS.
If this optional command is given, the wave-induced set-up is computed and accounted for in the wave
computations (during the computation it is added to the depth that is obtained from the READ BOTTOM
and READ WLEVEL commands).
This approximation in SWAN can only be applied to open coast (unlimited supply of water from outside
the domain, e.g. nearshore coasts) in contrast to closed basin, e.g. lakes and estuaries, where this option
should not be used.
Note that set-up is not computed correctly with spherical coordinates.
Note that set-up is not supported in case of parallel runs using either MPI or OpenMP!
| [supcor] | by default the wave-induced set-up is computed with a constant added such | |
| that the set-up is zero in the deepest point in the computational grid. The | ||
| user can modify this constant by the value of [supcor]. The user can thus | ||
| impose a set-up in any one point (and only one) in the computational grid | ||
| by first running SWAN, then reading the set-up in that point and adding or | ||
| subtracting the required value of [supcor] (in m; positive if the set-up has | ||
| to rise). | ||
| Default: [supcor]=0. |
DIFFRACtion [idiffr] [smpar] [smnum] [cgmod]

If this optional command is given, the diffraction is included in the wave computation.
But the diffraction approximation in SWAN does not properly handle diffraction in harbours
or in front of reflecting obstacles (see Scientific/Technical documentation). Behind breakwaters with a
down-wave beach, the SWAN results seem reasonable. The spatial resolution near (the tip of)
the diffraction obstacle should be 1/5 to 1/10 of the dominant wave length.
Without extra measures, the diffraction computations with SWAN often converge poorly or not at all. Two
measures can be taken:
![$\displaystyle E^n_{i,j} = E^{n-1}_{i,j} - a \left[ E_{i-1,j} + E_{i,j-1} -4E_{i,j} + E_{i+1,j} + E_{i,j+1} \right]^{n-1}
$](img109.png)
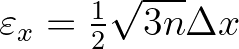 (recommended), the final width of the filter is
(recommended), the final width of the filter is
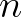 (in
(in 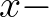 direction and similarly in
direction and similarly in 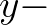 direction) and
direction) and 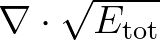 is the number of repetitions (see Scientific/Technical
documentation, Eq. (2.100)). Note that this smoothing option can not be applied in case of unstructured meshes.
is the number of repetitions (see Scientific/Technical
documentation, Eq. (2.100)). Note that this smoothing option can not be applied in case of unstructured meshes.
| [idiffr] | indicates the use of diffraction. If [idiffr]=0 then no diffraction is taken | |
| into account. | ||
| Default: [idiffr]=1. | ||
| [smpar] | smoothing parameter for the calculation of
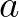 . During every . During every |
|
| smoothing step all grid points exchange [smpar] times the energy with their | ||
neighbours. Note that [smpar] is parameter 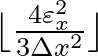 in the above text. in the above text. |
||
| Default: [smpar] = 0. | ||
| [smnum] | number of smoothing steps (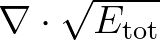 in the above text). For in the above text). For 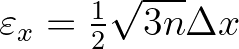 , it should be , it should be |
|
approximately equal to
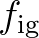 . . |
||
| Default: [smnum] = 0. | ||
| [cgmod] | adaption of propagation velocities in geographic space due to diffraction. | |
| If [cgmod]=0 then no adaption. | ||
| Default: [cgmod]=1. |
SURFBeat [df] [nmax] [emin] UNIForm/LOGarithmic

CANNOT BE USED IN CASE OF CURVILINEAR or UNSTRUCTURED GRIDS AND NOT IN 1D-MODE.
Using this optional command, the user activates the Infragravity Energy Module (IEM) of Reniers and Zijlema (2022).
Besides the energy balance equation for a sea-swell wave field, another energy balance is included to account for
the transfer of sea-swell energy to the bound infragravity (BIG) wave. This infragravity energy balance also involves
a nonlinear transfer, expressed by the biphase, through the phase coupling between the radiation stress forcing and the BIG wave.
For the prediction of the biphase for obliquely incident waves, an evolution equation is provided under the assumption that the bottom
slopes are mild and alongshore uniform.
The IEM framework is applied as follows. First, we assume that the conditions under which the surfbeat is modelled are stationary, and
that the overall prediction of the sea-swell and infragravity wave fields (both bound and free) is carried out with two COMPUTEs.
During the first COMPUTE both the short and bound long wave spectra are computed.
In this respect, the user specifies a frequency range for the sea-swell spectrum
that is bounded below by an infragravity frequency cut-off 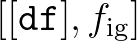 (see command CGRID).
Basically, this spectrum is subject to
propagation, shoaling, refraction, surf breaking and bottom friction (other processes should not be included).
In addition, an offshore directionally spread spectrum must be imposed on the west side of the
computational domain. (Currently, it is assumed that a regular grid is defined with the direction of the positive
(see command CGRID).
Basically, this spectrum is subject to
propagation, shoaling, refraction, surf breaking and bottom friction (other processes should not be included).
In addition, an offshore directionally spread spectrum must be imposed on the west side of the
computational domain. (Currently, it is assumed that a regular grid is defined with the direction of the positive 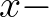 axis pointing eastward.)
axis pointing eastward.)
Next, to add BIG components with frequencies less than or equal to 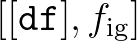 , the infragravity energy balance is solved. This equation is forced by bichromatic wave groups
related to all pairs in the sea-swell spectrum with a frequency difference less or equal to
, the infragravity energy balance is solved. This equation is forced by bichromatic wave groups
related to all pairs in the sea-swell spectrum with a frequency difference less or equal to 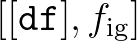 . In addition, this equation is solved in tandem with the evolution
equation for the biphase.
. In addition, this equation is solved in tandem with the evolution
equation for the biphase.
By the finish of the first COMPUTE, the user may include some plotting commands related to both the short and long wave spectra, including the integral parameters.
Finally, the BIG waves are assumed to reflect at the shoreline (on the east side of the domain).
Accordingly, the user must specify an obstacle line alongshore (parallel with 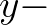 axis) with a reflection coefficient
(see command OBST REFL ... LINE ...; for reasons of consistency, the same obstacle line must be specified in the first COMPUTE with a transmission coefficient of 1,
so that the wave field will not be affected).
axis) with a reflection coefficient
(see command OBST REFL ... LINE ...; for reasons of consistency, the same obstacle line must be specified in the first COMPUTE with a transmission coefficient of 1,
so that the wave field will not be affected).
The reflected ig waves are assumed to be free and their evolution can be predicted by
the conventional energy balance equation during the second COMPUTE.
In view of this, a frequency range
![$[{\tt [df]},f_{\rm ig}]$](img117.png) must be specified which can be either uniform or logarithmic.
must be specified which can be either uniform or logarithmic.
| [df] | the constant size of BIG frequency bin (in Hz). | |
| Default: [df]=0.01. | ||
| [nmax] | the maximum number of short-wave pairs for creating bichromatic wave groups. | |
| Default: [nmax] = 50000. | ||
| [emin] | the energy threshold in fraction of energy spectrum peak. | |
| With this threshold one takes into account those short wave components to | ||
| create bichromatic wave groups while their energy levels are larger than | ||
[emin]
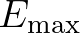 with with 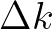 the peak of the spectrum. the peak of the spectrum. |
||
| Default: [emin] = 0.05. | ||
| UNIFORM | frequencies for reflected ig waves are uniformly distributed. | |
| This is the default. | ||
| LOGARITHMIC | frequencies for reflected ig waves are logarithmically distributed. |
SCAT [iqcm] &
( GRId [rfac] ) &
( TRUnc [alpha] [qmax] )

Using this optional command, the user activates a source term that allows for the generation and propagation of
cross correlations between scattered waves due to variations in the bathymetry and mean currents. Such variations are rapid
compared to the distance between the crossing waves (at the scale of 100 1000 m)
and is particularly relevant for cases involving narrowband waves (swells) in coastal regions with shallow water
and ambient currents. In turn, the immediate spatial effects of
coherent scattering, interference, refraction and diffraction can cause large-scale changes in the wave parameters.
1000 m)
and is particularly relevant for cases involving narrowband waves (swells) in coastal regions with shallow water
and ambient currents. In turn, the immediate spatial effects of
coherent scattering, interference, refraction and diffraction can cause large-scale changes in the wave parameters.
The underlying modelling concept has been introduced and developed by Smit and Janssen (2013), Smit et al. (2015a,b) and
Akrish et al. (2020) and is now known as the quasi-coherent (QC) model.
The QC framework has been made consistent with the action balance equation through the addition of a scattering source term
and is hereby adopted in the current operational version of SWAN (version 41.41). This source term involves
a convolution integral which relates the spectral representation of wave action, including cross correlations, and the response
of the small-scale medium variations (through the dispersion relation).
The modelling strategy by means of the QC scattering term provides the ability to readily nest a QC model into a conventional, regional-scale SWAN (or other spectral) model.
However, when setting up a QC model, other existing (shallow-water) source terms (e.g., surf breaking, triad wave-wave interactions)
should not be included as they do not account for the cross correlations among wave components of the scattered field and, in turn, their effects
on wave interference patterns.
Therefore, the user should be aware of the currently limited use of the QC model in support of the complete description of the wave field, including
the dissipation and nonlinear effects.
The inclusion of QC-consistent depth-induced wave breaking and nonlinear (triad) interactions will be considered in the near future
(see also Smit et al., 2015b and Smit and Janssen, 2016).
In order to apply the QC approximation properly, an incident wave spectrum must be imposed at the wave maker. This provides input used in defining
the coherent radius of the scattered wave field and in designating the grid spacing in wave number space. The definition of the coherent region is especially relevant
for the discrete Fourier transform of the modulation of the dispersion relation (owing to the medium variations). Furthermore, the grid domain in wave number space defines a region in which the effects
of cross correlations are resolved.
This will be constructed by SWAN with the aid of the discrete frequency-direction sector (see command CGRID SECTOR).
The associated resolution is determined by the characteristic width (or standard deviation) of the incoming spectrum, 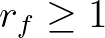 (in 1/m), and the user-defined resolution factor
(in 1/m), and the user-defined resolution factor 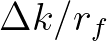 ,
and is expressed as
,
and is expressed as
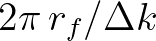 . The correlation (or coherent) length scale is then given by
. The correlation (or coherent) length scale is then given by
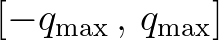 .
.
The unbounded convolution integral of the scattering source term is computed as the sum over a finite range of wave numbers. The extent of this range reflects
the scale to which variations in the medium (seabed and/or mean currents) affect the wave field. The convolution sum is thus limited to the range
![$[-q_{\rm max}\,,\,q_{\rm max}]$](img124.png) with
with 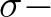 the maximum scattering wave number. This maximum can either be directly set or can be taken as a multiple of the mean wave number
at the wave maker.
the maximum scattering wave number. This maximum can either be directly set or can be taken as a multiple of the mean wave number
at the wave maker.
| [iqcm] | indicates the modelling and computation of QC scattering: | |
| = 0 no scattering | ||
| = 1 scattering due to non-uniform bathymetry and currents | ||
| (the latter only if applicable; see command INPGRID CURRENT) | ||
| = 2 wave-current interaction under the assumption of a slowly varying | ||
| bathymetry | ||
| Default: [iqcm] = 1. | ||
| GRID | with this option the user controls the grid resolution of the wave number | |
| space. It is defined as a multiple of the characteristic width of the | ||
| incoming wave spectrum. | ||
| [rfac] | the resolution factor through which the incident spectral width is | |
| multiplied. Note that this factor must be larger or equal 1. | ||
| Default: [rfac] = 1. | ||
| TRUNC | with this option the user truncates the infinite convolution sum at | |
| either the multiple of the mean wave number at the wave maker (the | ||
| default option), or at the maximum scattering wave number. When | ||
| specifying both parameters, then their mimimum is considered as the | ||
| final limit on the sum. | ||
| [alpha] | the coefficient by which the mean wave number is multiplied to set | |
| the limit on the convolution sum. | ||
| Default: [alpha] = 1. | ||
| [qmax] | the maximum scattering wave number (in 1/m). |
| WINDGrowth |
| |
| QUADrupl |
| |
| WCAPping |
OFF < >
| BREaking |
| |
| REFrac |
| |
| FSHift |
| |
| BNDCHK |

With this optional command the user can change the default inclusion of various physical processes (e.g.
for research purposes). This command is not recommended for operational use.
| WINDGROWTH | switches off wind growth (in commands GEN1, GEN2 and GEN3). | |
| QUADRUPL | switches off quadruplet wave-wave interactions (in command GEN3). | |
| WCAPPING | switches off whitecapping (in command GEN3). | |
| BREAKING | switches off depth-induced breaking dissipation. | |
| Caution: wave heights may diverge in very shallow water. | ||
| REFRAC | switches off refraction (action transport in 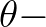 direction). direction). |
|
| FSHIFT | switches off frequency shifting in frequency space (action transport in 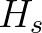 space). space). |
|
| BNDCHK | switches off the checking of the difference between imposed and computed | |
| significant wave height at the boundary of the computational grid (see also | ||
| command SET). |
The SWAN team 2024-09-09