Next: Output Up: Model description Previous: Physics Index
| BSBT
PROP < | Sec |
| GSE [waveage] < MIn >
| | HR |
| | DAy |

Command to choose:
| BSBT | the BSBT scheme will be used in the computations. | |
| GSE | garden-sprinkler effect is to be counteracted in the S&L propagation scheme | |
| (default for nonstationary regular grid computations) or in the propagation | ||
| scheme for unstructured grids by adding a diffusion term to the basic equation. | ||
| This may affect the numerical stability of SWAN (see Scientific/Technical | ||
| documentation). | ||
| [waveage] | the time interval used to determine the diffusion which counteracts the so-called | |
| garden-sprinkler effect. The default value of [waveage] is zero, i.e. no added | ||
| diffusion. The value of [waveage] should correspond to the travel time of | ||
| the waves over the computational region. |
NUMeric ( STOPC [dabs] [drel] [curvat] [npnts] &
| -> STAT [mxitst] [alfa] |
< > [limiter] ) &
| NONSTAT [mxitns] |
( DIRimpl [cdd] ) &
( SIGIMpl [css] [eps2] [outp] [niter] ) &
( CTheta [cfl] ) &
( CSigma [cfl] ) &
( SETUP [eps2] [outp] [niter] )

With this optional command the user can influence some of the numerical properties of SWAN.
| STOPC | With this option the user can influence the criterion for terminating the | |
| iterative procedure in the SWAN computations (both stationary and | ||
| nonstationary). The criterion make use of the second derivative, or curvature, | ||
| of the iteration curve of the significant wave height. As the solution of a | ||
| simulation approaches full convergence, the curvature of the iteration curve will | ||
tend to zero. SWAN stops the process if the relative change in 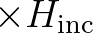 from one from one |
||
| iteration to the next is less than [drel] and the curvature of the iteration | ||
curve of 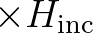 normalized with normalized with 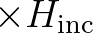 is less than [curvat] or the absolute change in is less than [curvat] or the absolute change in |
||
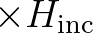 from one iteration to the next is less than [dabs]. Both conditions need to from one iteration to the next is less than [dabs]. Both conditions need to |
||
| be fulfilled in more than fraction [npnts]% of all wet grid points. | ||
| With respect to the QC modelling, another stopping criteria will be employed. | ||
Namely, SWAN stops the iteration process if the absolute change in 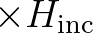 from one from one |
||
iterate to another is less than [dabs]
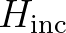 , where , where 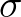 is the representative is the representative |
||
incident wave height, or the relative change in 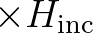 from one to the next iteration from one to the next iteration |
||
| is less than [drel]. These criteria must be fulfilled in more than [npnts]% of | ||
| all active, well-defined points. | ||
| [dabs] | Default: [dabs] = 0.005 [m] or [dabs] = 0.05 [ ] in case of QC model. ] in case of QC model. |
|
| [drel] | Default: [drel] = 0.01 [ ] ] |
|
| [curvat] | Default: [curvat] = 0.005 [ ] ] |
|
| Note that [curvat] is not used in the QC model. | ||
| [npnts] | Default: [npnts] = 99.5 [ ] ] |
|
| STAT | indicates the use of parameters in a stationary computation. | |
| [mxitst] | the maximum number of iterations for stationary computations. | |
| The computation stops when this number is exceeded. | ||
| Default: [mxitst] = 50. | ||
| Note that [mxitst] can be set to 0 if one wants to check the input to the | ||
| model without making computations. | ||
| [alfa] | proportionality constant used in the frequency-dependent under-relaxation | |
| technique. Based on experiences, a suggestion for this parameter is [alfa] = 0.01. | ||
| In case of diffraction computations, the use of this parameter is recommended. | ||
| Default: [alfa] = 0.00. | ||
| NOT MEANINGFUL FOR NONSTATIONARY COMPUTATIONS. | ||
| NONSTAT | indicates the use of parameters in a nonstationary computation. | |
| [mxitns] | the maximum number of iterations per time step for nonstationary computations. | |
| The computation moves to the next time step when this number is exceeded. | ||
| Default: [mxitns] = 1. | ||
| Note that [mxitns] can be set to 0 if one wants to check the input to the | ||
| model without making computations. | ||
| [limiter] | determines, in both stationary and nonstationary runs, the maximum change per | |
iteration of the energy density per spectral (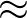 , ,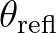 )-bin, given in )-bin, given in |
||
| terms of a fraction of the omni-directional Phillips level (see Scientific/ | ||
| Technical documentation). | ||
| Default: [limiter] = 0.1. | ||
| DIRIMPL | this option is used to influence the numerical scheme for refraction. | |
| [cdd] | A value of [cdd]=0 corresponds to a central scheme and has the largest | |
accuracy (diffusion 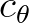 0) but the computation may more easily generate 0) but the computation may more easily generate |
||
| spurious fluctuations. A value of [cdd]=1. corresponds to a first order | ||
| upwind scheme and it is more diffusive and therefore preferable if (strong) | ||
| gradients in depth or current are present. | ||
| Default: [cdd] = 0.5. | ||
| SIGIMPL | controls the accuracy of computing the frequency shifting and the stopping criterion | |
| and amount of output for the SIP solver (used in the computations in the presence | ||
| of currents or time varying depth). | ||
| CTHETA | this option prevents an excessive directional turning at a single grid point or vertex | |
| due to a very coarse bathymetry or current locally. This option limits the directional | ||
turning rate 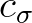 based on the CFL restriction. (See Eq. 3.41 of Scientific/ based on the CFL restriction. (See Eq. 3.41 of Scientific/ |
||
| Technical documentation). See also the final remark in Section 2.6.3. | ||
| Note that if this command is not specified, then the limiter is not activated. | ||
| [cfl] | upper limit for the CFL restriction for 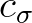 . A suggestion for this parameter is . A suggestion for this parameter is |
|
| [cfl] = 0.9. | ||
| Default: [cfl] = 0.9 (when command CTHETA is activated). | ||
| CSIGMA | this option prevents an excessive frequency shifting at a single grid point or vertex | |
| due to a very coarse bathymetry or current locally. This option limits the frequency | ||
shifting rate 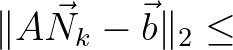 based on the CFL restriction. See also the final remark in Section based on the CFL restriction. See also the final remark in Section |
||
| 2.6.3. Note that if this command is not specified, then the limiter is not activated. | ||
| [cfl] | upper limit for the CFL restriction for 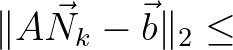 . A suggestion for this parameter is . A suggestion for this parameter is |
|
| [cfl] = 0.9. | ||
| Default: [cfl] = 0.9 (when command CSIGMA is activated). | ||
| SETUP | controls the stopping criterion and amount of output for the SOR solver in the | |
| computation of the wave-induced set-up. | ||
| [css] | A value of [css]=0 corresponds to a central scheme and has the largest | |
accuracy (diffusion 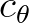 0) but the computation may more easily generate 0) but the computation may more easily generate |
||
| spurious fluctuations. A value of [css]=1. corresponds to a first order upwind | ||
| scheme and it is more diffusive and therefore preferable if (strong) gradients in | ||
| depth or current are present. | ||
| Default: [css] = 0.5. | ||
| [eps2] | Relative stopping criterion to terminate the linear solver (SIP or SOR). The | |
| criterion for the SIP solver is based on |
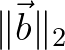 [eps2] [eps2]
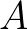 |
|
where 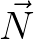 is a matrix, is a matrix, 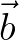 is the action density vector, is the action density vector, 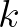 is the right hand vector is the right hand vector |
||
and 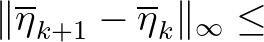 is the iteration number. is the iteration number. |
||
The criterion for the SOR solver is based on
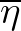 [eps2] where [eps2] where |
||
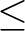 is the set-up. is the set-up. |
||
| Default: [eps2] = 1.e-4 in case of SIP and [eps2] = 1.e-6 in case of SOR. | ||
| [outp] | output for the iterative solver: | |
| 0 = no output | ||
| 1 = additional information about the iteration process is written to the PRINT file | ||
| 2 = gives a maximal amount of output concerning the iteration process | ||
| 3 = summary of the iteration process | ||
| Default: [outp] = 0. | ||
| [niter] | maximum number of iterations for the linear solver. | |
| Default: [niter] = 20 in case of SIP and [niter] = 1000 in case of SOR. |
The SWAN team 2024-09-09