Next: Diffraction Up: Modelling of obstacles Previous: Reflection
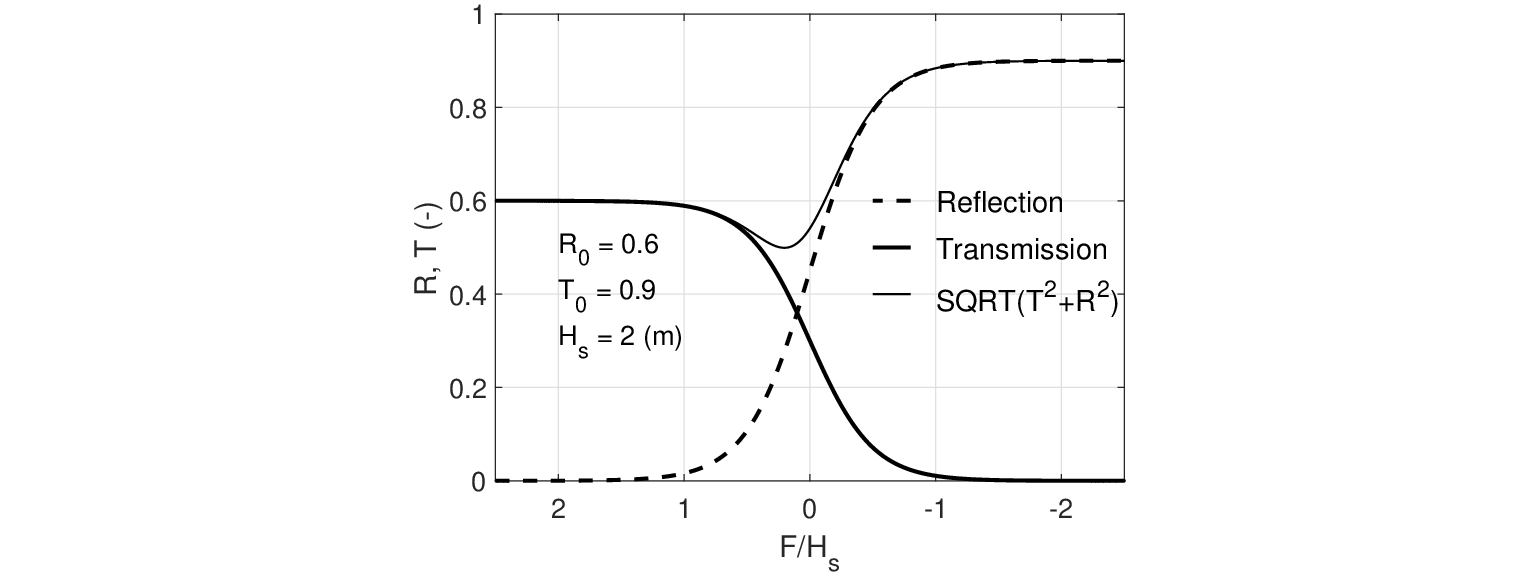
In case an obstacle becomes flooded, its reflection and transmission properties change as a function of the relative freeboard, defined as the ratio of the difference in dam height and the water level by the (incident) significant wave height, i.e. 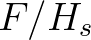 . For transmission this dependence can be schematized as described in Section 2.5.1, where transmission increases with increasing freeboard. Another method is to scale the fixed reflection and fixed transmission coefficients as a function of the relative freeboard. This dependence is expressed using a tanh function in which a parameter
. For transmission this dependence can be schematized as described in Section 2.5.1, where transmission increases with increasing freeboard. Another method is to scale the fixed reflection and fixed transmission coefficients as a function of the relative freeboard. This dependence is expressed using a tanh function in which a parameter 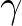 is employed to define the range (in terms of the relative freeboard) over which the fixed reflection and/or transmission coefficients varies between their minimum and maximum values. This dependency is given by
is employed to define the range (in terms of the relative freeboard) over which the fixed reflection and/or transmission coefficients varies between their minimum and maximum values. This dependency is given by
![$\displaystyle R = \left [ 1 +\tanh \left ( \frac{2}{\gamma_{\tiny\mbox{R}}} \frac{F}{H_s} \right ) \right ] \frac{R_0}{2}
$](img640.png) (2.176)
(2.176)
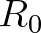 , and
, and
![$\displaystyle T = \left [ 1 +\tanh \left ( -\frac{2}{\gamma_{\tiny\mbox{T}}} \frac{F}{H_s} \right ) \right ] \frac{T_0}{2}
$](img642.png) (2.177)
(2.177)
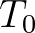 .
.
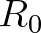 has a value of 0.6, and that the maximum or fixed transmission coefficient is equal to
has a value of 0.6, and that the maximum or fixed transmission coefficient is equal to 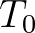 = 0.9. In this example the significant wave height has a value of 2 m. The structure of above equations is such that the parameters
= 0.9. In this example the significant wave height has a value of 2 m. The structure of above equations is such that the parameters
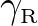 and
and
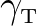 coincide with the positions where the reflection and transmission coefficient have their minimum or maximum value.
coincide with the positions where the reflection and transmission coefficient have their minimum or maximum value.
 |
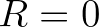 and the transmission coefficient
and the transmission coefficient 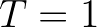 .
.
The SWAN team 2024-09-09