Next: Computation of force in Up: Numerical approaches Previous: Implementation of QC approximation
A curvilinear grid is characterized by the co-ordinates of the grid points, i.e.
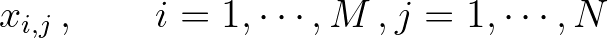 (3.89)
(3.89)
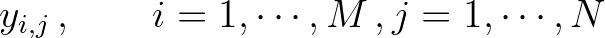 (3.90)
(3.90)
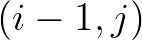 and
and 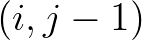 are used to compute the action densities
in the point
are used to compute the action densities
in the point 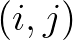 . Numerical approximations are obtained by a two-dimensional Taylor expansion with respect to the point
. Numerical approximations are obtained by a two-dimensional Taylor expansion with respect to the point
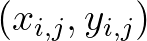 .
.
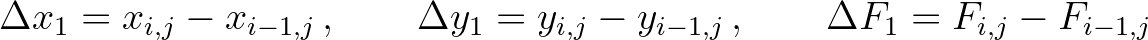 (3.91)
(3.91)
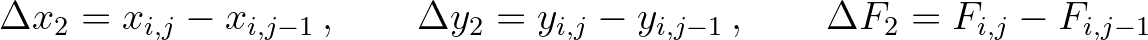 (3.92)
(3.92)
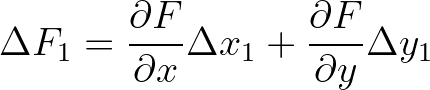 (3.93)
(3.93)
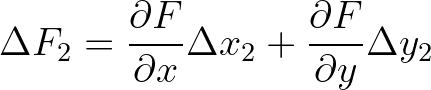 (3.94)
(3.94)
![$\displaystyle \frac{\partial F}{\partial x} \approx \frac{\Delta y_2 \Delta F_1 - \Delta y_1 \Delta F_2}{[D]}
$](img1187.png) (3.95)
(3.95)
![$\displaystyle \frac{\partial F}{\partial y} \approx \frac{\Delta x_1 \Delta F_2 - \Delta x_2 \Delta F_1}{[D]}
$](img1188.png) (3.96)
(3.96)
![$\displaystyle [D] = \Delta y_2 \Delta x_1 - \Delta y_1 \Delta x_2
$](img1189.png) (3.97)
(3.97)
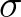 and
and 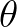 temporarily) read
temporarily) read
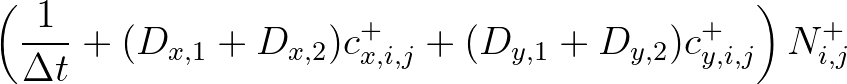 |
|||
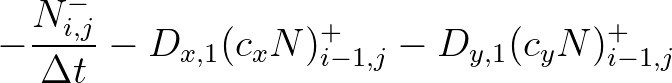 |
|||
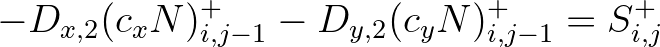 |
(3.98) |
![$\displaystyle D_{x,1} = \frac{\Delta y_2}{[D]} \, , \quad
D_{y,1} = -\frac{\De...
...D_{x,2} = -\frac{\Delta y_1}{[D]} \, , \quad
D_{y,2} = \frac{\Delta x_1}{[D]}
$](img1193.png) (3.99)
(3.99)
 denotes the new time level
denotes the new time level 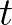 , and
, and  the old time level
the old time level 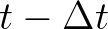 . The equation for a stationary computation is found
by putting
. The equation for a stationary computation is found
by putting 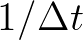 to 0.
to 0.
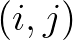 is enclosed between the lines connecting this point
with its neighbours
is enclosed between the lines connecting this point
with its neighbours 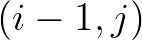 and
and 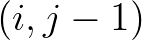 . It can be shown that this is the case if
. It can be shown that this is the case if
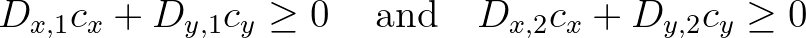 (3.100)
(3.100)
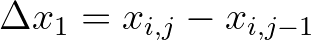 , etc. and
, etc. and
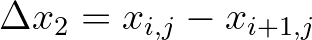 , etc. In the third sweep,
, etc. In the third sweep,
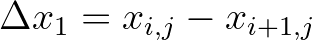 , etc. and
, etc. and
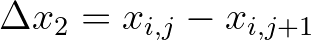 , etc. In the fourth sweep,
, etc. In the fourth sweep,
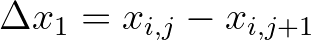 , etc. and
, etc. and
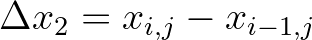 , etc. Otherwise, all of the above equations and conditions remain
the same.
, etc. Otherwise, all of the above equations and conditions remain
the same.
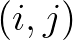 ,
, 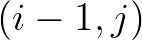 and
and 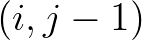 .
If for each side of this triangle the energy flux is computed as the inner product of the average of
.
If for each side of this triangle the energy flux is computed as the inner product of the average of 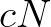 and an inward-pointing normal of the side itself, then the
three energy fluxes are exactly in balance assuming that the situation is stationary, and the source term is zero. In this case it is found that
and an inward-pointing normal of the side itself, then the
three energy fluxes are exactly in balance assuming that the situation is stationary, and the source term is zero. In this case it is found that
![$\displaystyle \left [ c_x N \right ]_{i,j}^{+} (\Delta y_2 - \Delta y_1) + \lef...
...]_{i-1,j}^{+} (-\Delta y_2) +
\left [ c_x N \right ]_{i,j-1}^{+} (\Delta y_1) +$](img1205.png) |
|||
![$\displaystyle \left [ c_y N \right ]_{i,j}^{+} (\Delta x_1 - \Delta x_2) + \lef...
...{i-1,j}^{+} (\Delta x_2) +
\left [ c_y N \right ]_{i,j-1}^{+} (-\Delta x_1) = 0$](img1206.png) |
(3.101) |
The SWAN team 2024-09-09