Next: Numerical treatment of obstacles Up: Numerical approaches Previous: Governing equations in curvilinear
FORCE is the wave-driven stress, i.e. the force per unit surface driving the wave-driven current, expressed in N/m , is defined
as the derivative of the radiation stresses
, is defined
as the derivative of the radiation stresses
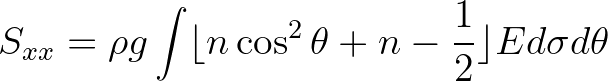 (3.102)
(3.102)
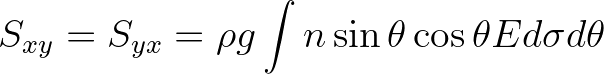 (3.103)
(3.103)
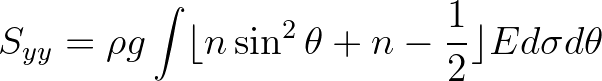 (3.104)
(3.104)
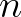 is the ratio of group velocity and phase velocity, that is,
is the ratio of group velocity and phase velocity, that is,
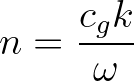 (3.105)
(3.105)
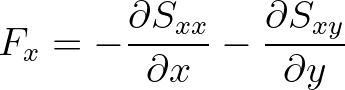 (3.106)
(3.106)
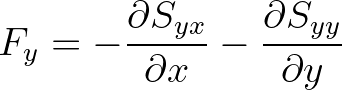 (3.107)
(3.107)
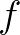 be one of the components of the tensor. We have to derive expressions for
be one of the components of the tensor. We have to derive expressions for
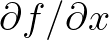 and
and
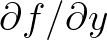 . Derivatives with respect to the computational grid co-ordinates
. Derivatives with respect to the computational grid co-ordinates 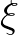 and
and 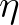 can easily be found. The transformation is based on
can easily be found. The transformation is based on
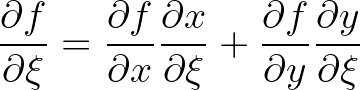 (3.108)
(3.108)
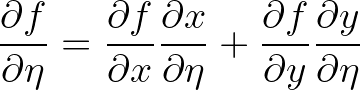 (3.109)
(3.109)
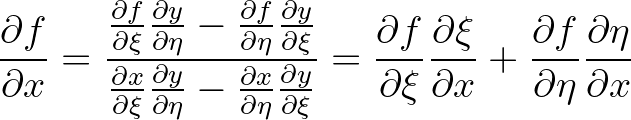 (3.110)
(3.110)
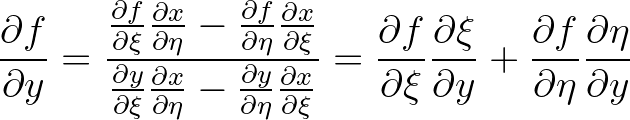 (3.111)
(3.111)
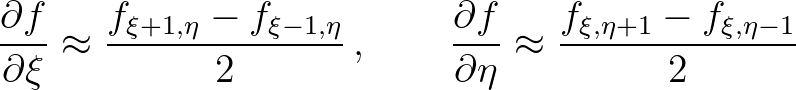 (3.112)
(3.112)
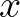 and
and 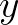 . On the boundaries of the computational region a one-sided approximation can be used.
. On the boundaries of the computational region a one-sided approximation can be used.
The SWAN team 2024-09-09