Next: Integration over Up: Numerical approaches Previous: Numerical treatment of obstacles
In the procedure for obstacles it is necessary to determine the crossing point of the obstacle and a grid line in the computational grid.
The obstacle is composed of straight sides. Let one side have the end points
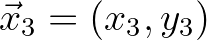 and
and
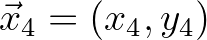 .
The end points of the grid line (both computational grid points) are
.
The end points of the grid line (both computational grid points) are
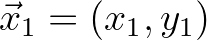 and
and
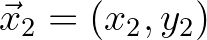 . The crossing point must obey the following equation
. The crossing point must obey the following equation
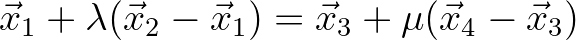 (3.114)
(3.114)
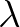 and
and 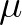 must be between 0 and 1. It follows that
must be between 0 and 1. It follows that
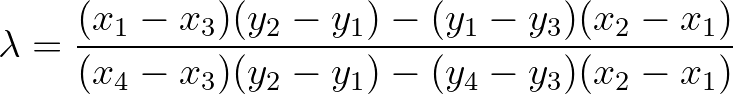 (3.115)
(3.115)
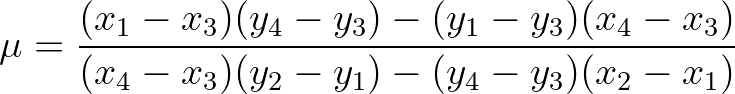 (3.116)
(3.116)