Internally, SWAN use action density as function of direction and relative (angular) frequency. Users may want
to obtain results in terms of absolute frequency, if only because measurements were taken at fixed positions.
Two modifications of the SWAN model that were needed to supply the information to the users are
- the computation of integrated quantities such as average absolute frequency and
- the transformation of action or energy density.
The average absolute frequency is determined as follows
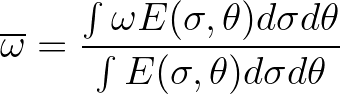 (3.126)
(3.126)
The transformation of action or energy density from relative frequency 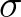 to absolute frequency
to absolute frequency 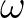 is complicated because the mapping is not one-to-one, and therefore the Jacobian can become infinite. The
value of
is complicated because the mapping is not one-to-one, and therefore the Jacobian can become infinite. The
value of 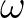 is determined by
is determined by
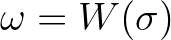 .
.
The transformation is designed such that the following requirements are met.
- If current velocities tend to zero the action densities for absolute frequency become identical
with the densities with respect to relative frequency.
- The total energy density with respect to relative density is identical with the total energy density
with respect to absolute density.
Furthermore, it is assumed that the distribution of absolute frequencies is the same as the distribution of
relative frequencies.
In the continuous model the mapping is done by
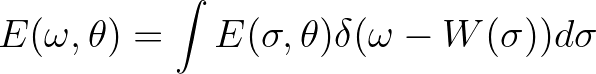 (3.127)
(3.127)
This relation is discretized whereby the energy density is assumed to be constant over intervals from
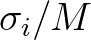 to
to 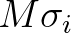 .
.
The SWAN team 2024-09-09
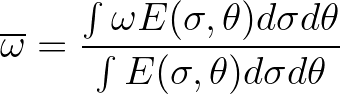 (3.126)
(3.126)
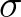 to absolute frequency
to absolute frequency 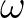 is complicated because the mapping is not one-to-one, and therefore the Jacobian can become infinite. The
value of
is complicated because the mapping is not one-to-one, and therefore the Jacobian can become infinite. The
value of 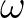 is determined by
is determined by
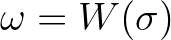 .
.
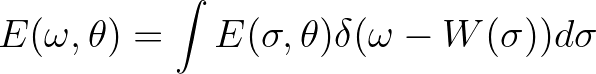 (3.127)
(3.127)
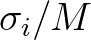 to
to 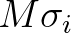 .
.