Next: Computation of breaking source Up: Numerical approaches Previous: Transformation from relative to
The interpolation of spectra in SWAN, both in space and time, is a slight modification of the procedure
as used in WAM. This procedure is not a simple (spectral) bin-by-bin interpolation because that would cause
reduction of the spectral peak if the peaks of the original spectra do not coincide. It is an interpolation
where the spectra are first normalized by average frequency and direction, then interpolated and then
transformed back.
The average frequencies of the two origin spectra are determined using the frequency moments of the
spectra
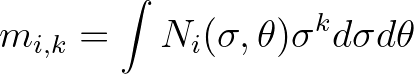 (3.128)
(3.128)
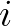 =1,2 (the two origin
spectra) and
=1,2 (the two origin
spectra) and 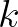 =0,1 (the zero- and first frequency moments of these spectra). Then
=0,1 (the zero- and first frequency moments of these spectra). Then
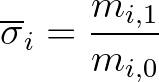 (3.129)
(3.129)
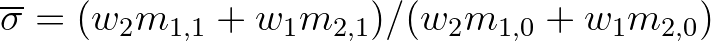 (3.130)
(3.130)
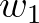 is the relative distance (in space or time) from the interpolated spectrum to the first
origin spectrum
is the relative distance (in space or time) from the interpolated spectrum to the first
origin spectrum
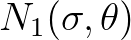 and
and 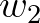 is the same for the second origin spectrum
is the same for the second origin spectrum
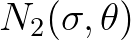 . Obviously,
. Obviously,
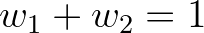 .
.
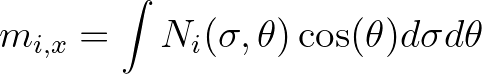 (3.131)
(3.131)
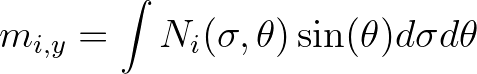 (3.132)
(3.132)
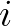 =1,2. The average direction is then
=1,2. The average direction is then
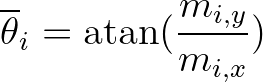 (3.133)
(3.133)
![$\displaystyle \overline{\theta} = \mbox{atan} [\frac{w_{2} m_{1,y} + w_{1} m_{2,y}}{w_{2} m_{1,x} + w_{1} m_{2,x}}]
$](img1284.png) (3.134)
(3.134)
![$\displaystyle N(\sigma,\theta) = w_{2} N_{1} [\overline{\sigma}_{1} \sigma/\ove...
...ma /
\overline{\sigma}, \theta - (\overline{\theta}-{\overline{\theta}}_{2})]
$](img1285.png) (3.135)
(3.135)
The SWAN team 2024-09-09