Next: Wave boundary and initial Up: Numerical approaches Previous: Interpolation of spectra
The surf breaking dissipation of Battjes and Janssen (1978) reads
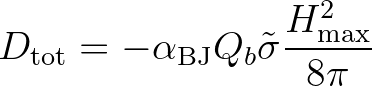 (3.136)
(3.136)
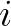 is
is
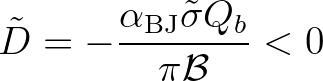 (3.138)
(3.138)
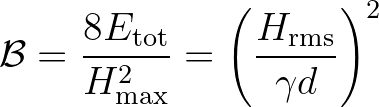 (3.139)
(3.139)
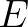 (since
(since 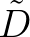 depends on
depends on 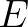 through
through 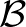 ), we apply the Newton linearisation
to approximate the source term at iteration level
), we apply the Newton linearisation
to approximate the source term at iteration level 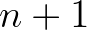 , as follows
, as follows
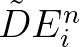 , is replaced by
, is replaced by
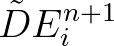 . This preserves positivity of energy density
. This preserves positivity of energy density 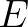 , if the following
inequality holds
, if the following
inequality holds
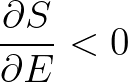 (3.141)
(3.141)
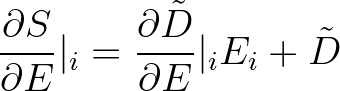 (3.142)
(3.142)
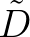 is a function of
is a function of 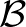 which is proportional to
which is proportional to 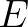 , so
, so
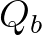 is a function of
is a function of 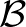 , we get (using the quotient rule)
, we get (using the quotient rule)
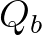 is found by differentiating this with respect to
is found by differentiating this with respect to  :
:
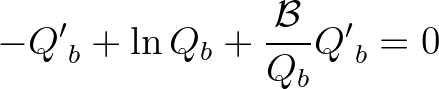 (3.146)
(3.146)
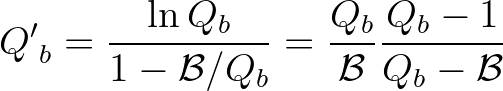 (3.147)
(3.147)
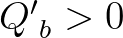 , because
, because 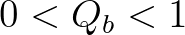 and
and
 .
Substitution in (3.144) gives
.
Substitution in (3.144) gives
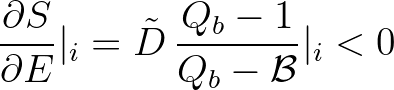 (3.148)
(3.148)
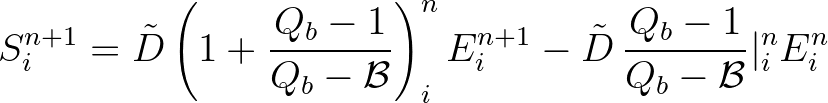 (3.149)
(3.149)
The SWAN team 2024-09-09