Wave boundary and initial conditions
To obtain the numerical solution of the action balance equation (2.16), the wave boundary
and initial conditions should be provided. The incoming wave components at the up-wave
boundaries in the SWAN model are specified by a two-dimensional spectrum. Several
options are available:
- A parametric one-dimensional spectrum with a certain imposed directional distribution.
An example is a Jonswap spectrum.
- A discrete one-dimensional spectrum with a certain imposed directional distribution.
This is often obtained from measurements.
- A discret two-dimensional spectrum. This may be obtained from other SWAN runs or other
models, e.g. WAM and WAVEWATCH III.
For the parametric one-dimensional spectrum, the following optional forms have been recommended:
a Pierson-Moskowitz spectrum (Pierson and Moskowitz, 1964), a Jonswap spectrum
(Hasselmann et al., 1973) and a Gaussian-shaped spectrum.
The boundaries in frequency space are fully absorbing at the lowest and the highest discrete
frequency. So, energy can freely propagate across these boundaries and thus total energy
might not be conserved in some cases. However, a diagnostic tail 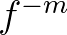 (
(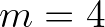 or
or 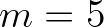 )
is added above the high frequency cut-off, which is used to compute nonlinear wave-wave
interactions at the high frequencies and to compute integral wave parameters. When the directional
space is a closed circular, no directional boundary conditions are needed. However,
for reasons of economy, SWAN has an option to compute only wave components in a pre-defined
directional sector. In this case, the boundaries of this sector are fully absorbing (action
density might be removed from the model by refraction).
)
is added above the high frequency cut-off, which is used to compute nonlinear wave-wave
interactions at the high frequencies and to compute integral wave parameters. When the directional
space is a closed circular, no directional boundary conditions are needed. However,
for reasons of economy, SWAN has an option to compute only wave components in a pre-defined
directional sector. In this case, the boundaries of this sector are fully absorbing (action
density might be removed from the model by refraction).
To facilitate the integration process of the action balance equation, wave boundary conditions
in geographical space need to be provided. The boundaries of the computational grid in SWAN
are either land or water. In case of land there is no problem. The land does not generate waves
and in SWAN it absorbs all incoming wave energy. But in the case of a water boundary there is
a problem. If observations are available, they can be used as inputs at the boundary. In case
no wave conditions are given along the boundary, SWAN assumes that no waves enter the model
and waves can leave the model freely along that boundary. This assumption results in errors.
Therefore, to get reliable results, especially for such case, the model boundaries must be placed
far away from the area of interest.
In case of nonstationary computation, the default initial spectra are computed from the local
wind velocities using the deep-water growth curve of Kahma and Calkoen (1992), cut off at values
of significant wave height and peak frequency from Pierson and Moskowitz (1964). The average
(over the model area) spatial step size is used as fetch with local wind. The shape of the
spectrum is default Jonswap with a
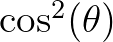 directional distribution centred around
the local wind direction.
directional distribution centred around
the local wind direction.
The first guess conditions of a stationary run of SWAN are default determined with the second
generation mode of SWAN.
It is possible to obtain an initial state by carrying out a previous stationary or nonstationary
computation.
The SWAN team 2024-09-09
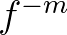 (
(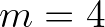 or
or 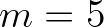 )
is added above the high frequency cut-off, which is used to compute nonlinear wave-wave
interactions at the high frequencies and to compute integral wave parameters. When the directional
space is a closed circular, no directional boundary conditions are needed. However,
for reasons of economy, SWAN has an option to compute only wave components in a pre-defined
directional sector. In this case, the boundaries of this sector are fully absorbing (action
density might be removed from the model by refraction).
)
is added above the high frequency cut-off, which is used to compute nonlinear wave-wave
interactions at the high frequencies and to compute integral wave parameters. When the directional
space is a closed circular, no directional boundary conditions are needed. However,
for reasons of economy, SWAN has an option to compute only wave components in a pre-defined
directional sector. In this case, the boundaries of this sector are fully absorbing (action
density might be removed from the model by refraction).
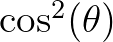 directional distribution centred around
the local wind direction.
directional distribution centred around
the local wind direction.