Introduction

In some large-scale applications SWAN is known to produce seemingly unstable results. One of the causes is the coarseness of the grid $-$ usually the unstructured one. This issue will be dealt with in Section 3.8.5. Another cause is the fully implicit treatment of the refraction term when dealing with non-stationary runs. Implicit schemes allow propagation of wave energy using a large time step. 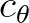In this treatment the value of $c_\theta$ is determined at the point where the action density is to be updated. If this value does vary too much over one time step, causality may not be preserved. Usually, this is not the case in small scale coastal applications.


In large scale oceanic applications, however, the depth may vary from one grid point to the next by a factor of over 10 (e.g. in presence of seamounts). Then the value of 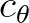$c_\theta$ at the shallowest grid point is not representative anymore of the interval between the two grid points, and it is justified to limit the value to one that is representative. The problem now is to find a limitation which on the one hand guarantees smooth behaviour in large-scale applications and which has no influence on small-scale applications. This will be elaborated in Section 3.8.3.


Related to the aforementioned problems we first elaborate the consequences of the law of constant energy flux along the wave ray (Whitham, 1974) in the next section.